Перейти к содержанию

Руководство пользователя по OpenSCAD/Язык сценариев OpenSCAD

Материал из Викиучебника — открытых книг для открытого мира


Язык сценариев OpenSCAD

[править]

Общие сведения

[править]

Шаблон:Incomplete

Вступление

[править]

OpenSCAD это программа 2D/3D и твердотельного моделирования которая основанная на функциональном программном языке используемая для создания моделей которые можно отобразить на экране и отрэндерить в 3D сетку, что позволяет модель экспортировать в различные 2D/3D форматы файлов.

Скрипт на языке OpenSCAD используется для создания 2D или 3D моделей. Этот скрипт представляет собой свободно форматируемый список действий с выражениями. 

 object();
 variable = value;
 operator()   action();
 operator() { action();    action(); }
 operator()   operator() { action(); action(); }
 operator() { operator()   action();
              operator() { action(); action(); } }
Объекты

Объекты являются строительными блоками для моделей, созданных с помощью 2D и 3D примитивов. Объекты заканчиваются точкой с запятой ';'.

Действия

Действия с выражениями включают создание объектов использующих примитивы и присвоение значений переменным. Действия с выражениями также заканчиваются точкой с запятой ";".

Операторы

Операторы, или преобразования, изменяют местоположение, цвет и другие свойства объектов. Операторы используют фигурные скобки "{}", когда их область действия охватывает более одного действия. Для одного действия или группы действий можно использовать более чем один оператор. Несколько операторов обрабатываются справа налево, то есть оператор, ближайший к действию, обрабатывается первым. Операторы не заканчиваются точкой с запятой ";", но отдельные действия, которые они содержат, заканчиваются. 

 Примеры
  
   cube(5);
   x = 4+y;
   rotate(40) square(5,10);
   translate([10,5]) { circle(5); square(4); }
   rotate(60) color("red") { circle(5); square(4); }
   color("blue") { translate([5,3,0]) sphere(5); rotate([45,0,45]) { cylinder(10); cube([5,6,7]); } }

Комментарии

[править]

Комментарии — это способ оставлять заметки в сценарии или коде (либо для себя, либо для будущих программистов), описывающий, как работает код или что он делает. Комментарии не обрабатываются компилятором и не должны использоваться для описания самоочевидного кода.

OpenSCAD использует C++-стиль комментариев: 

// Это комментарий
  
myvar = 10; // Остальная часть строки - это комментарий
  
/*
   Многострочные комментарии
   могут охватывать несколько строк.
*/

Значения и типы данных

[править]

Значение в OpenSCAD - это либо число (например, 42), логическое значение (например, true), строка (например, "foo"), диапазон (например, [0:1:10]), вектор (например, [1,2,3]) или Неопределенное значение (undef). Значения могут храниться в переменных, передаваться в качестве аргументов функции и возвращаться в виде результатов функции.

[OpenSCAD - это динамически типизированный язык с фиксированным набором типов данных. Здесь нет имен типов и нет определяемых пользователем типов. Функции не являются значениями. На самом деле переменные и функции занимают непересекающиеся пространства имен.]

Числа

[править]

Числа являются наиболее важным типом данных в OpenSCAD, и они записываются в привычной десятичной системе счисления, используемой в других языках. Например, -1, 42, 0,5, 2,99792458e+8. [OpenSCAD не поддерживает восьмеричную или шестнадцатеричную запись чисел.]

В дополнение к десятичным числам определены следующие имена для специальных чисел:

  • PI

В OpenSCAD есть только один тип чисел, который представляет собой 64-разрядное число IEEE с плавающей запятой. [OpenSCAD не различает целые числа и числа с плавающей запятой как два разных типа и не поддерживает комплексные числа.] Поскольку OpenSCAD использует стандарт IEEE с плавающей запятой, то существует несколько отклонений от поведения чисел в математике:

  • Мы используем двоичную систему с плавающей точкой. Дробное число не представляется точно, если только знаменатель не равен степени 2. Например, 0.2 (2/10) не имеет точного внутреннего представления, но 0.25 (1/4) и 0.125 (1/8) представлены точно.
  • Наибольшее представимое число составляет около 1e308. Если числовой результат слишком велик, то результатом может быть бесконечность (печатаемая как inf в echo).
  • Наименьшее представимое число составляет около -1e308. Если числовой результат слишком мал, то результатом может быть -бесконечность (печатаемая как -inf в echo).
  • Если числовой результат недействителен, то результат может быть не ч1ислом (англ.: Not A Number) (печатаемая как nan в echo).
  • Если ненулевой числовой результат слишком близок к нулю, чтобы быть представимым, то результат равен -0, если результат отрицательный, в противном случае он равен 0. Ноль (0) и отрицательный ноль (-0) обрабатываются как два разных числа некоторыми математическими операциями и печатаются в 'echo' по-разному, хотя они сравниваются как равные.

Константы "inf" и "nan" не поддерживаются OpenSCAD в качестве числовых констант, хотя вы можете вычислять числа, которые печатаются таким образом с помощью "echo". Вы можете определить переменные с этими значениями используя: 

inf = 1e200 * 1e200;
nan = 0 / 0;
echo(inf,nan);

Значение 'nan' - это единственное значение OpenSCAD, которое не равно никакому другому значению, включая его самого. Хотя вы можете проверить, имеет ли переменная 'x' неопределенное значение, используя 'x==undef', вы не можете использовать 'x==0/0', чтобы проверить, не является ли x числом. Вместо этого вы должны использовать 'x != x', чтобы проверить, является ли x nan.

Логические значения

[править]

Логические значения - это значения истинности. Существует два логических значения, а именно true (истина) и false (ложь). Логическое значение передается в качестве аргумента условному выражению 'if()'. условному оператору '? :', и логическим операторам '!' (нет), '&&' (и) и '||' (или). In all of these contexts, you can actually pass any quantity. Большинство значений преобразуются в "истину" в логическом контексте, значения, которые считаются "ложными", являются:

  • false
  • 0 and -0
  • ""
  • []
  • undef

Обратите внимание, что "false" (строка), [0] (числовой вектор), [ [] ] (вектор, содержащий пустой вектор), [false] (вектор, содержащий логическое значение false) и 0/0 (не число (Not A Number(nan))) все считаются истинными.

Строки

[править]

Строка - это последовательность из нуля или более символов юникода. Строковые значения используются для указания имен файлов при импорте файла и для отображения текста в целях отладки при использовании echo(). Строки также можно использовать с новым примитивом text() добавленном в 2015.03.

Строковый литерал записывается как последовательность символов, заключенных в кавычки ", например: "" (пустая строка), или "это строка".

Чтобы включить символ " в строковый литерал, используйте \". Чтобы включить символ \ в строковый литерал, используйте \\. В строковых литералах можно использовать следующие escape-последовательности, начинающиеся с \:

  • \" → "
  • \\ → \
  • \t → табуляция
  • \n → новая строка
  • \r → возврат каретки
  • \u03a9 → Ω - смотри text() для получения дополнительной информации о символах юникода

Примечание: Это поведение является новым с версии OpenSCAD-2011.04. Вы можете обновить старые файлы с помощью следующей команды sed: sed 's/\\/\\\\/g' non-escaped.scad > escaped.scad 

 Пример:
  
 echo("The quick brown fox \tjumps \"over\" the lazy dog.\rThe quick brown fox.\nThe \\lazy\\ dog.");
  
 Результат

   ECHO: "The quick brown fox     jumps "over" the lazy dog.
   The quick brown fox.
   The \lazy\ dog."
  
 Старый результат

   ECHO: "The quick brown fox \tjumps \"over\" the lazy dog.
   The quick brown fox.\nThe \\lazy\\ dog."

Диапазоны

[править]

Диапазоны используются в циклах for() и в children(). У них есть 2 разновидности:

[<начало>: <конец>]
[<начало>: <прирост>: <конец>]

Хотя они заключены в квадратные скобки [], они не являются векторами. Они используют двоеточия : для разделителей, а не запятые. 

r1 = [0:10];
r2 = [0.5:2.5:20];
echo(r1); // ECHO: [0: 1: 10]
echo(r2); // ECHO: [0.5: 2.5: 20]

Вам следует избегать значений шага, которые не могут быть представлены точно в виде двоичных чисел с плавающей запятой. Целые числа в порядке, как и дробные значения, знаменатель которых равен степени двух. Например, 0,25 (1/4) и 0,125 (1/8) безопасны, но следует избегать 0,2 (2/10). Проблема с этими значениями шага заключается в том, что в вашем диапазоне может быть слишком много или слишком мало элементов из-за неточной арифметики.

Пропущенный <прирост> по умолчанию равняется 1. Диапазон в форме [<начало>:<конец>] с <началом> больше, чем <конец>, генерирует предупреждение и эквивалентен [<конец>: 1: <начало>]. Диапазон в форме [<начало>:1:<конец>] с <началом> больше, чем <конец>, не генерирует предупреждение и эквивалентен []. <Приращение> в диапазоне может быть отрицательным (для версий после 2014 года).

Неопределенное Значение

[править]

Неопределенное (англ.: undefined) значение - это специальное значение, записанное как undef. Это начальное значение переменной, которой не было присвоено значение, и оно часто возвращается в результате функций или операций, которым передаются недопустимые аргументы. Наконец, undef может использоваться в качестве нулевого значения, эквивалентного null или NULL на других языках программирования.

Все арифметические выражения, содержащие undef значения оцениваются как undef. В логических выражениях, undef эквивалентен false. Выражения оператора отношения с undef оцениваются как false, за исключением undef==undef, который является true.

Обратите внимание, что числовые операции могут также возвращать 'nan' (not-a-number(не число)), чтобы указать на недопустимый аргумент. Например, 0/false это undef, но 0/0 это 'nan'. Операторы отношений, такие как < and > возвращают false если передаются недопустимые аргументы. Хотя undef является значением языка, 'nan' - нет.

Переменные

[править]

Переменные OpenSCAD создаются оператором с именем или идентификатором, присваиванием с помощью выражения и точки с запятой. Роль массивов, встречающихся во многих императивных языках, обрабатывается в OpenSCAD при использовании векторов. 

var = 25;
xx = 1.25 * cos(50);
y = 2*xx+var;
logic = true;
MyString = "Это строка";
a_vector = [1,2,3];
rr = a_vector[2];      // член вектора
range1 = [-1.5:0.5:3]; // for() диапазон циклов
xx = [0:5];            // альтернативный for() диапазон циклов

OpenSCAD - это функциональный язык программирования, как таковые переменные привязаны к выражениям и сохраняют одно значение в течение всего срока службы из-за требований ссылочной прозрачности. В императивных языках, таких как C, то же поведение рассматривается как константы, которые обычно противопоставляются обычным переменным.

Другими словами, переменные OpenSCAD больше похожи на константы, но с важным отличием. Если переменным присваивается значение несколько раз, во всех местах кода используется только последнее присвоенное значение. См. Дальнейшее обсуждение в Переменные устанавливаются во время компиляции, а не во время выполнения. Такое поведение связано с необходимостью для поддержки входа переменных через командную строку, с помощью параметра -D переменная=значение. В настоящее время OpenSCAD помещает это присваивание в конец исходного кода и, следовательно, должен позволять изменять значение переменной для этой цели.

Значения не могут быть изменены во время выполнения; все переменные фактически являются константами, которые не изменяются. Каждая переменная сохраняет свое последнее присвоенное значение во время компиляции в соответствии с Функциональными языками программирования. В отличие от императивных языков, таких как C, OpenSCAD iне является итеративным языком, и поэтому концепция x = x + 1 неверна. Понимание этой концепции ведет к пониманию красоты OpenSCAD.

До версии 2015.03

Невозможно было выполнять назначения в любом месте, кроме верхнего уровня файла и верхнего уровня модуля. Внутри if/else  или for  цикла, assign() был необходим.

Начиная с версии 2015.03

Переменные теперь можно назначать в любой области. Обратите внимание, что назначения допустимы только в той области, в которой они определены - вам по-прежнему не разрешается передавать значения во внешнюю область. См. Область действия переменных для получения более подробной информации. 

a=0;
if (a==0) 
  {
 a=1; //  до 2015.03 эта строка будет выдавать Ошибку Компиляции
      //  с 2015.03 больше не является ошибкой, но значение a=1 ограничено фигурными скобками {}
  }

Неопределенная переменная

[править]

Неназначенная переменная имеет специальное значение undef. Он может быть проверен в условном выражении и возвращен функцией. 

 Пример:
  
 echo("Переменная a", a);                        // Переменная a не определена
 if (a==undef) {
   echo("Переменная a является неопределенной"); // Переменная a является неопределенной
 }

Область действия переменных

[править]

Когда такие операторы, как translate() и color(), должны охватывать более одного действия (действия заканчиваются на ;), фигурные скобки {} необходимы для группировки действий, создавая новую внутреннюю область. Когда есть только одна точка с запятой, фигурные скобки обычно необязательны.

Каждая пара фигурных скобок создает новую область внутри области, в которой они используются. Начиная с 2015.03, в этой новой области можно создавать новые переменные. Новые значения могут быть присвоены переменным, которые были созданы во внешней области. Эти переменные и их значения также доступны для других внутренних областей, созданных в этой области, но "недоступны" для чего-либо за пределами этой области. Переменные по-прежнему содержат только последнее значение, присвоенное в пределах области. 

                       // область 1
 a = 6;                // создать a
 echo(a,b);            //                6, undef
 translate([5,0,0]){   // область 1.1
   a= 10;
   b= 16;              // создать b
   echo(a,b);          //              100, 16   a=10; был переопределен более поздним a=100;
   color("blue") {     // область 1.1.1
     echo(a,b);        //              100, 20
     cube();
     b=20;
   }                   // возврат в 1.1
   echo(a,b);          //              100, 16
   a=100;              // переопределить a в 1.1
 }                     // возврат в 1   
 echo(a,b);            //                6, undef
 color("red"){         // область 1.2
   cube();
   echo(a,b);          //                6, undef
 }                     // возврат в 1
 echo(a,b);            //                6, undef
  
 //В этом примере области 1 и 1.1 являются внешними областями для 1.1.1, а 1.2 - нет.
Анонимные области не считаются областями:
 {
   angle = 45;
 }
 rotate(angle) square(10);

Циклы for() не являются исключением из правила о переменных, имеющих только одно значение в области видимости. Для каждого прохода создается копия содержимого цикла. Каждому проходу присваивается своя область действия, что позволяет любым переменным иметь уникальные значения для этого прохода. Нет, вы все еще не можете сделать a=a+1;

Переменные задаются во время компиляции, а не во время выполнения

[править]

Поскольку OpenSCAD вычисляет значения своих переменных во время компиляции, а не во время выполнения, последнее назначение переменной в области применяется везде в этой области или ее внутренних областях. Возможно, было бы полезно думать о них как о переопределяемых константах, а не как о переменных. 

// Значение 'a' отражает только последнее установленное значение
   a = 0;
   echo(a);  // 5
   a = 3;
   echo(a);  // 5
   a = 5;

Хотя это кажется нелогичным, это позволяет вам делать некоторые интересные вещи: например, если вы настроили файлы общей библиотеки так, чтобы значения по умолчанию определялись как переменные на их корневом уровне, когда вы включаете этот файл в свой собственный код, вы можете 'переопределить' эти константы, просто присвоив им новое значение. Таким образом, изменение постоянных значений дает вам больше гибкости. Если константы никогда не изменятся, конечно, вы всегда можете быть уверены, что у вас есть значение, которое вы видите в любом определении константы. Здесь все не так. Если вы видите определение постоянного значения в любом другом месте, его значение может быть другим. Это очень гибкий подход.

Специальные переменные

[править]

Специальные переменные предоставляют альтернативные средства передачи аргументов модулям и функциям. Все переменные, начинающиеся с '$' являются специальными переменными, подобными специальным переменным в lisp. Как таковые, они более динамичны, чем обычные переменные. (для получения более подробной информации см. Другие языковые функции)

Векторы

[править]

Вектор или список - это последовательность из нуля или более значений OpenSCAD. Векторы представляют собой набор числовых или логических значений, переменных, векторов, строк или любой их комбинации. Они также могут быть выражениями, которые оценивают одно из них. Векторы выполняют роль массивов, найденных во многих императивных языках. Приведенная здесь информация также относится к спискам и таблицам, которые используют векторы для своих данных.

Вектор имеет квадратные скобки, [] заключающие ноль или более элементов (элементов или членов), разделенных запятыми. Вектор может содержать векторы, которые содержат векторы и т.д.


Примеры:
   [1,2,3]
   [a,5,b]
   []
   [5.643]
   ["a","b","string"]
   [[1,r],[x,y,z,4,5]]
   [3, 5, [6,7], [[8,9],[10,[11,12],13], c, "string"]
   [4/3, 6*1.5, cos(60)]

использование в OpenSCAD: 

  cube( [width,depth,height] );           // дополнительные пробелы, показанны для ясности
  translate( [x,y,z] )
  polygon( [ [x0,y0],  [x1,y1],  [x2,y2] ] );
Создание

Векторы создаются путем написания списка элементов, разделенных запятыми и заключенных в квадратные скобки. Переменные заменяются их значениями. 

  cube([10,15,20]);
  a1 = [1,2,3];
  a2 = [4,5];
  a3 = [6,7,8,9];
  b  = [a1,a2,a3];    // [ [1,2,3], [4,5], [6,7,8,9] ]  обратите внимание на увеличенную глубину вложенности
Индексирование элементов в векторах
[править]

Элементы в векторах пронумерованы от 0 до n-1, где n - длина, возвращаемая len(). Адреса элементов внутри векторов со следующем обозначением: 

e[5]           // элемент № 5 (шестой)      1-го уровня вложенности
e[5][2]        // элемент 2 элемента 5      2-го уровня вложенности
e[5][2][0]     // элемент 0 из 2 из 5       3-го уровня вложенности
e[5][2][0][1]  // элемент 1 из 0 из 2 из 5  4-го уровня вложенности
примеры элементов с длинами из len()
e = [ [1], [], [3,4,5], "string", "x", [[10,11],[12,13,14],[[15,16],[17]]] ];  // length 6

адрес         длина   элемент
e[0]          1       [1]
e[1]          0       []
e[5]          3       [ [10,11], [12,13,14], [[15,16],[17]] ]
e[5][1]       3       [ 12, 13, 14 ]
e[5][2]       2       [ [15,16], [17] ]
e[5][2][0]    2       [ 15, 16 ]
e[5][2][0][1] undef   16
    
e[3]          6       "string"
e[3 ][2]      1       "r"
  
s = [2,0,5]; a = 2;
s[a]          undef   5
e[s[a]]       3       [ [10,11], [12,13,14], [[15,16],[17]] ]
Индексация точечных обозначений
[править]

К первым трем элементам вектора можно получить доступ с помощью альтернативной точечной нотации: 

e.x    //равнозначно e[0]
e.y    //равнозначно e[1]
e.z    //равнозначно e[2]
Векторные операторы
[править]
concat
[править]

Шаблон:Requires

concat() cобъединяет элементы 2 или более векторов в один вектор. Никаких изменений в уровне вложенности не делается. 

 vector1 = [1,2,3]; vector2 = [4]; vector3 = [5,6];
 new_vector = concat(vector1, vector2, vector3); // [1,2,3,4,5,6]
  
 string_vector = concat("abc","def");                 // ["abc", "def"]
 one_string = str(string_vector[0],string_vector[1]); // "abcdef"
len
[править]

len() это функция, которая возвращает длину векторов или строк. Индексы элементов находятся в диапазоне от [0] до [длина-1].

вектор
Возвращает количество элементов на этом уровне.
Единичные значения, которые являются не not векторами, возвращает undef.
строка
Возвращает количество символов в строке.
 a = [1,2,3]; echo(len(a));   //  3

См. Примеры элементов с длиной

Матрица
[править]

Матрица - это вектор векторов. 

Пример, который определяет двумерную матрицу вращения
mr = [
     [cos(angle), -sin(angle)],
     [sin(angle),  cos(angle)]
    ];

Получение входных данных

[править]

Теперь у нас есть переменные, было бы неплохо иметь возможность вводить их вместо того, чтобы задавать значения из кода. Существует несколько функций для чтения данных из файлов DXF, или вы можете установить переменную с помощью переключателя -D в командной строке.

Получение точки из рисунка

Получение точки полезно для считывания исходной точки в 2D-виде на техническом чертеже. Функция dxf_cross считывает пересечение двух линий на указанном вами слое и возвращает точку пересечения. Это означает, что точка должна быть задана двумя строками в файле DXF, а не точечным объектом. 

OriginPoint = dxf_cross(file="drawing.dxf", layer="SCAD.Origin", 
                        origin=[0, 0], scale=1);

Получение значения измерения

Вы можете прочитать размеры из технического чертежа. Это может быть полезно для считывания угла поворота, высоты выдавливания или расстояния между деталями. На чертеже создайте размер, в котором отображается не значение размера, а идентификатор. Чтобы прочитать значение, вы указываете этот идентификатор в своей программе: 

TotalWidth = dxf_dim(file="drawing.dxf", name="TotalWidth",
                        layer="SCAD.Origin", origin=[0, 0], scale=1);

Для наглядного примера обеих функций см. Example009 и изображение на домашней странице OpenSCAD.

Примитивы объемных тел

[править]

Куб

[править]

cube() создает куб в первом октанте. Когда параметр center=true куб центрируется в начале координат. Имена аргументов являются необязательными, если они заданы в указанном здесь порядке. 

cube(size = [x,y,z], center = true/false);
cube(size =  x ,     center = true/false);
Параметры :
size
одно значение, куб со всеми сторонами этой длины
массив из 3-х значений [x, y, z], куб с размерами x, y и z.
center
false (по умолчанию), 1-й (положительный) октант, первый угол находится на (0,0,0)
true, куб центрирован на (0,0,0)
значения по умолчанию:  cube();   выводит:  cube(size = [1, 1, 1], center = false);
примеры :

равнозначные описания для этого примера
 cube(size = 18);
 cube(18);
 cube([18,18,18]);
 .
 cube(18,false);
 cube([18,18,18],false);
 cube([18,18,18],center=false);
 cube(size = [18,18,18], center = false);
 cube(center = false,size = [18,18,18] );


равнозначные описания для этого примера
 cube([18,28,8],true);
 box=[18,28,8];cube(box,true);

Сфера

[править]

Создает сферу в начале системы координат. Имя аргумента r является необязательным. Чтобы использовать d вместо r, d должен быть назван.

Параметры

r
Радиус. Это радиус сферы. Разрешение сферы зависит от размера сферы и переменных $fa, $fs и $fn. Для получения дополнительной информации об этих специальных переменных смотрите: OpenSCAD_User_Manual/Other_Language_Features
d
Диаметр. Это диаметр сферы.
$fa
Угол наклона фрагмента в градусах
$fs
Размер фрагмента в миллиметрах
$fn
Разрешение
 значения по умолчанию:  sphere();   выводит:   sphere($fn = 0, $fa = 12, $fs = 2, r = 1);

Примеры использования 

sphere(r = 1);
sphere(r = 5);
sphere(r = 10);
sphere(d = 2);
sphere(d = 10);
sphere(d = 20);

// результатом будет сфера радиусом 2мм, с поверхностью высокого разрешения
sphere(2, $fn=100); 

// также создается сфера радиусом 2мм, с поверхностью высокого разрешения, но у этой
// не так много маленьких треугольников на полюсах сферы
sphere(2, $fa=5, $fs=0.1);

Sample OpenSCAD spheres, showing clearly the difference in scale.

Цилиндр

[править]

cylinder() создает цилиндр или конус с центром вокруг оси z. Если значение center равно true, оно также центрируется вертикально вдоль оси z.

Имена параметров являются необязательными, если они заданы в указанном здесь порядке. Если параметр получил имя, то все следующие параметры также должны быть поименованы.

ПРИМЕЧАНИЕ: Если используются r, d, d1 или d2, они должны быть названы. 

cylinder(h = height, r1 = BottomRadius, r2 = TopRadius, center = true/false);
Параметры
h : высота цилиндра или конуса
r : радиус цилиндра. r1 = r2 = r.
r1 : радиус, нижней части конуса.
r2 : радиус, верхней части конуса.
d : диаметр цилиндра. r1 = r2 = d / 2. Шаблон:Требуется
d1 : диаметр, нижней части конуса. r1 = d1 / 2. Шаблон:Требуется
d2 : диаметр, верхней части конуса. r2 = d2 / 2. Шаблон:Требуется
center
false (по умолчанию), z в диапозоне от 0 до h
true, z в диапозоне от -h/2 до +h/2
$fa : минимальный угол (в градусах) каждого фрагмента.
$fs : минимальная длина окружности каждого фрагмента.
$fn : исправлено количество фрагментов в 360 градусах. Значения 3 или более переопределяют значения $fa и $fs
$fa, $fs и $fn должны быть именованными параметрами. нажмите здесь для получения более подробной информации.
значения по умолчанию: cylinder();  выводит: cylinder($fn = 0, $fa = 12, $fs = 2, h = 1, r1 = 1, r2 = 1, center = false);


равнозначные описания для этого примера
 cylinder(h=15, r1=9.5, r2=19.5, center=false);
 cylinder(  15,    9.5,    19.5, false);
 cylinder(  15,    9.5,    19.5);
 cylinder(  15,    9.5, d2=39  );
 cylinder(  15, d1=19,  d2=39  );
 cylinder(  15, d1=19,  r2=19.5);


равнозначные описания для этого примера
 cylinder(h=15, r1=10, r2=0, center=true);
 cylinder(  15,    10,    0,        true);
 cylinder(h=15, d1=20, d2=0, center=true);
  • center = false
    center = false
  • center = true
    center = true
равнозначные описания для этого примера
 cylinder(h=20, r=10, center=true);
 cylinder(  20,   10, 10,true);
 cylinder(  20, d=20, center=true);
 cylinder(  20,r1=10, d2=20, center=true);
 cylinder(  20,r1=10, d2=2*10, center=true);
использование $fn

Большие значения $fn создают более гладкие, более круглые поверхности за счет увеличения времени рендеринга. Некоторые используют средние значения во время разработки для более быстрого рендеринга, а затем меняют значение на большое для окончательного рендеринга F6.

Однако использование малых значений может привести к появлению некоторых интересных некруглых объектов. Здесь показано несколько примеров: 

описания для этих примеров
 cylinder(20,20,20,$fn=3);
 cylinder(20,20,00,$fn=4);
 cylinder(20,20,10,$fn=4);
отверстия меньшего размера

Используя cylinder() с difference() для размещения отверстий в объектах, создаются отверстия меньшего размера. Это происходит потому, что круговые пути аппроксимируются многоугольниками, вписанными внутри круга. Точки многоугольника находятся на окружности, но прямые линии между ними находятся внутри. Чтобы все отверстия были больше истинного круга, многоугольник должен лежать полностью за пределами круга (описанного). Модули для описанных отверстий 

описание для этого примера
 poly_n = 6;
 color("blue") translate([0, 0, 0.02]) linear_extrude(0.1) circle(10, $fn=poly_n);
 color("green") translate([0, 0, 0.01]) linear_extrude(0.1) circle(10, $fn=360);
 color("purple") linear_extrude(0.1) circle(10/cos(180/poly_n), $fn=poly_n);

Многогранник

[править]

Многогранник - это наиболее общее трехмерное простейшее твердое тело. Его можно использовать для создания любой правильной или неправильной фигуры, в том числе с вогнутыми и выпуклыми частями. Изогнутые поверхности аппроксимируются несколькими плоскими поверхностями. 

polyhedron( points = [ [X0, Y0, Z0], [X1, Y1, Z1], ... ], triangles = [ [P0, P1, P2], ... ], convexity = N);        // до 2014.03
polyhedron( points = [ [X0, Y0, Z0], [X1, Y1, Z1], ... ], faces = [ [P0, P1, P2, P3, ...], ... ], convexity = N);   // 2014.03 & позже
Параметры
points
Вектор 3d точек или вершин. Каждая точка, в свою очередь, является вектором [x, y, z] своих координат.
Точки могут быть определены в любом порядке. N точек указываются в определённом порядке, от 0 до N-1.
triangles Шаблон:OpenSCAD User Manual/Deprecated
Вектор граней, которые в совокупности охватывают твердое тело. Каждая грань представляет собой вектор, содержащий индексы (на основе 0) 3 точек из вектора точек.
faces Шаблон:Требует
Вектор граней, которые в совокупности охватывают твердое тело. Каждая грань представляет собой вектор, содержащий индексы (на основе 0) 3 или более точек из вектора точек.
Грани могут быть определены в любом порядке. Определите достаточное количество граней, чтобы полностью охватить твердое тело без перекрытия.
Если точки, описывающие одну грань, не находятся в одной плоскости, грань автоматически разбивается на треугольники по мере необходимости.
convexity
Целое число. Параметр выпуклости указывает максимальное количество граней, через которые может пройти луч, пересекающий объект. Этот параметр необходим только для корректного отображения объекта в режиме предварительного просмотра OpenCSG. Это никак не влияет на рендеринг многогранника. При проблемах с отображением значение 10 должно работать нормально в большинстве случаев.
 значения по умолчанию: polyhedron(); выводит: polyhedron(points = undef, faces = undef, convexity = 1);

Вы можете начать с любой точки, но все грани должны иметь точки, расположенные в одном и том же направлении. OpenSCAD предпочитает по часовой стрелке, когда смотрит на каждую грань снаружи внутрь. Задняя часть просматривается сзади, нижняя часть снизу и т.д. Еще один способ запомнить это требование к порядку - использовать правило правой руки. Используя правую руку, поднимите большой палец вверх и согните пальцы, как бы показывая большой палец вверх, направьте большой палец в грань и расположите точки в направлении, в котором сгибаются ваши пальцы. Попробуйте сделать это на примере ниже.


Пример 1 Использование многогранника для создания куба( [ 10, 7, 5 ] );
номера точек у куба
развернутые грани куба
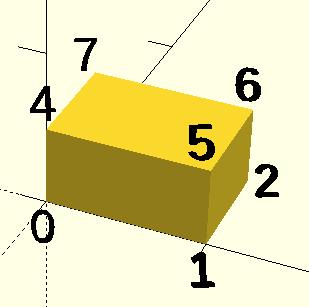
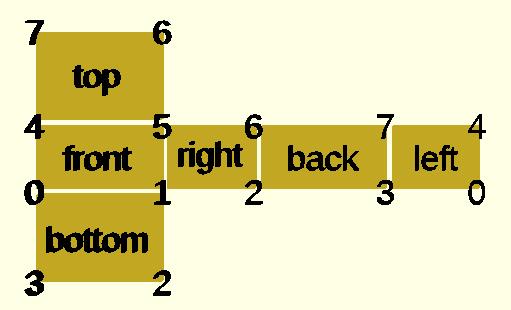
CubePoints = [
  [  0,  0,  0 ],  //0
  [ 10,  0,  0 ],  //1
  [ 10,  7,  0 ],  //2
  [  0,  7,  0 ],  //3
  [  0,  0,  5 ],  //4
  [ 10,  0,  5 ],  //5
  [ 10,  7,  5 ],  //6
  [  0,  7,  5 ]]; //7
  
CubeFaces = [
  [0,1,2,3],  // bottom
  [4,5,1,0],  // front
  [7,6,5,4],  // top
  [5,6,2,1],  // right
  [6,7,3,2],  // back
  [7,4,0,3]]; // left
  
polyhedron( CubePoints, CubeFaces );

равнозначные описания нижней грани
  [0,1,2,3],
  [0,1,2,3,0],
  [1,2,3,0],
  [2,3,0,1],
  [3,0,1,2],
  [0,1,2],[2,3,0],   // 2 треугольника без перекрытия
  [1,2,3],[3,0,1],
  [1,2,3],[0,1,3],
Пример 2 Пирамида с квадратным основанием:
Простая многогранная пирамида с квадратным основанием
polyhedron(
  points=[ [10,10,0],[10,-10,0],[-10,-10,0],[-10,10,0], // четыре точки в основании
           [0,0,10]  ],                                 // точка вершины 
  faces=[ [0,1,4],[1,2,4],[2,3,4],[3,0,4],              // все стороны треугольников
              [1,0,3],[2,1,3] ]                         // два триугольника для квадратного основания
 );
Пример 3 Треугольная призма:
Многогранная треугольная призма
   module prism(l, w, h){
       polyhedron(
               points=[[0,0,0], [l,0,0], [l,w,0], [0,w,0], [0,w,h], [l,w,h]],
               faces=[[0,1,2,3],[5,4,3,2],[0,4,5,1],[0,3,4],[5,2,1]]
               );
       
       // предварительный просмотр развернутый (не включайте в свою функцию)
       z = 0.08;
       separation = 2;
       border = .2;
       translate([0,w+separation,0])
           cube([l,w,z]);
       translate([0,w+separation+w+border,0])
           cube([l,h,z]);
       translate([0,w+separation+w+border+h+border,0])
           cube([l,sqrt(w*w+h*h),z]);
       translate([l+border,w+separation+w+border+h+border,0])
           polyhedron(
                   points=[[0,0,0],[h,0,0],[0,sqrt(w*w+h*h),0], [0,0,z],[h,0,z],[0,sqrt(w*w+h*h),z]],
                   faces=[[0,1,2], [3,5,4], [0,3,4,1], [1,4,5,2], [2,5,3,0]]
                   );
       translate([0-border,w+separation+w+border+h+border,0])
           polyhedron(
                   points=[[0,0,0],[0-h,0,0],[0,sqrt(w*w+h*h),0], [0,0,z],[0-h,0,z],[0,sqrt(w*w+h*h),z]],
                   faces=[[1,0,2],[5,3,4],[0,1,4,3],[1,2,5,4],[2,0,3,5]]
                   );
       }
   
   prism(10, 5, 3);

Отладка многогранников

[править]

Ошибки при определении многогранников включают в себя отсутствие всех граней с одинаковым порядком, перекрытие граней и отсутствие граней или частей граней. Как правило, грани многогранника также должны удовлетворять нескольким условиям:

  • ровно две грани должны встретиться на любом ребре многогранника.
  • Если две грани имеют общую вершину, то они должны быть в в том же цикле грань-ребра вокруг вершины.

Первое правило исключает многогранники, такие как два куба с общим ребром, а не герметичные модели; второе исключает многогранники, такие как два куба с общей вершиной.

При взгляде снаружи точки, описывающие каждую грань, должны располагаться в одном и том же порядке. OpenSCAD предпочитает CW (clockwise - по Часовой Стрелке) и предоставляет механизм для обнаружения CCW (counterclockwise - Против Часовой Стрелки). Когда комбинированный вид (F12) используется с F5, грани ПЧС (CCW) отображаются розовым цветом. Измените порядок точек для неправильных граней. Поверните объект, чтобы просмотреть все грани. Розовый вид можно отключить с помощью F10.

OpenSCAD позволяет временно закомментировать часть описаний граней, чтобы отображались только оставшиеся грани. Используйте //, чтобы закомментировать остальную часть строки. Используйте /* и */, чтобы начать и закончить блок комментариев. Это может быть частью строки или распространяться на несколько строк. Просмотр только части граней может быть полезным при определении правильных точек для отдельной грани. Обратите внимание, что твердое тело не отображается, только грани. При использовании F12 все грани имеют одну розовую сторону. Комментирование некоторых граней помогает также показать любое внутреннюю грань.

пример 1, показывающий только 2 грани
CubeFaces = [
/* [0,1,2,3],  // bottom
   [4,5,1,0],  // front */
   [7,6,5,4],  // top
/* [5,6,2,1],  // right
   [6,7,3,2],  // back */
   [7,4,0,3]]; // left


После определения многогранника его предварительный просмотр может показаться правильным. Один только многогранник может даже хорошо отрисоваться. Однако, чтобы убедиться, что это допустимое множество и что оно может генерировать допустимый файл STL, объедините его с любым кубом и визуализируйте его (F6). Если многогранник исчезает, это означает, что он неправильный. Пересмотрите порядок намотки всех граней и два правила, изложенные выше.

Неправильно направленные грани

[править]
Пример 4 более сложный многогранник с неправильно упорядоченными гранями

Если вы выберете 'Всё вместе (Thrown together) [F12]' в меню Вид (View) и скомпилируйте дизайн [F5] (не компелировать и рендер! [F6]) предварительный просмотр покажет выделением неправильно направленные полигоны. К сожалению, это выделение невозможно в режиме предварительного просмотра OpenCSG, поскольку это помешало бы реализации режима предварительного просмотра OpenCSG.

Ниже вы можете увидеть код и изображение такого проблемного многогранника, плохие полигоны (грани или сочетания граней) окрашены в розовый цвет. 

// Плохой многогранник
polyhedron
    (points = [
	       [0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60], 
	       [10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
	       ], 
     faces = [
		  [0,2,3],   [0,1,2],  [0,4,5],  [0,5,1],   [5,4,2],  [2,4,3],
                  [6,8,9],  [6,7,8],  [6,10,11], [6,11,7], [10,8,11],
		  [10,9,8], [0,3,9],  [9,0,6], [10,6, 0],  [0,4,10],
                  [3,9,10], [3,10,4], [1,7,11],  [1,11,5], [1,7,8],  
                  [1,8,2],  [2,8,11], [2,11,5]
		  ]
     );
Многогранник с плохо направленными многоугольниками

Правильный многогранник был бы следующим: 

polyhedron
    (points = [
	       [0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60], 
	       [10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
	       ], 
     faces = [
		  [0,3,2],  [0,2,1],  [4,0,5],  [5,0,1],  [5,2,4],  [4,2,3],
                  [6,8,9],  [6,7,8],  [6,10,11],[6,11,7], [10,8,11],
		  [10,9,8], [3,0,9],  [9,0,6],  [10,6, 0],[0,4,10],
                  [3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,8,7],  
                  [2,8,1],  [8,2,11], [5,11,2]
		  ]
     );
Совет для начинающих

Если вы действительно не понимаете "ориентацию", попробуйте определить неправильно ориентированные розовые грани, а затем перевернуть последовательность ссылок на векторы точек, пока не получите правильное отображение. К примеру, в приведенном выше примере третий треугольник([0,4,5]) был неправильным, и мы исправили это так [4,0,5]. Помните, что список граней - это круговой список. Кроме того, вы можете выбрать "Показать ребра" в меню "Вид", распечатать снимок экрана и пронумеровать как точки, так и грани. В нашем примере точки помечены черным цветом, а грани - синим. Переверните объект и при необходимости сделайте вторую копию с обратной стороны. Таким путём вы сможете держать верное направление (This way you can keep track).

Техника по часовой стрелке

Ориентация определяется круговым указанием по часовой стрелке. Это означает, что если вы смотрите на треугольник (в этом случае [4,0,5]) снаружи вы увидите, что путь проходит по часовой стрелке вокруг центра грани. Порядок намотки [4,0,5] по часовой стрелке и, следовательно, хорошо. Порядок намотки [0,4,5] против часовой стрелки и, следовательно, плохо. Аналогично, любой другой порядок по часовой стрелке [4,0,5] работает: [5,4,0] и [0,5,4] тоже хорошо. Если вы используете технику по часовой стрелке, ваши грани всегда будут снаружи (за пределами OpenSCAD, хотя другие программы используют против часовой стрелки в качестве внешней стороны).

Думайте об этом как о Правиле Левой Руки:

Если вы положите левую руку на грань, согнув пальцы в направлении порядка точек, ваш большой палец должен быть направлен наружу. Если ваш большой палец указывает внутрь, вам нужно изменить порядок намотки.

Многогранник с плохо ориентированными многоугольниками


Краткое описание 'Многогранника' 

* Точки определяют все точки/вершины фигуры.
* Грани - это список плоских многоугольников, соединяющих точки/вершины.

Каждая точка в списке точек определяется с помощью 3-мерной x,y,z характеристики положения. Точки в списке точек автоматически перечисляются, начиная с нуля, для использования в списке граней (0,1,2,3,... и т.д.).

Каждая грань в списке граней определяется путем выбора 3 или более точек (с использованием порядкового номера точек) из списка точек.

например, faces=[ [0,1,2] ] определяет треугольник из первой точки (точки равны нулю) ко второй точке, а затем к третьей точке.

При взгляде на любую грань снаружи, на ней должны быть перечислены все точки в порядке по часовой стрелке.

Повторения точек в списке точек многогранника

[править]

Список точек определения многогранника может содержать повторы. Когда две или более точки имеют одинаковые координаты, они считаются одной и той же вершиной многогранника. Итак, следующий многогранник: 

points = [[ 0, 0, 0], [10, 0, 0], [ 0,10, 0],
          [ 0, 0, 0], [10, 0, 0], [ 0,10, 0],
          [ 0,10, 0], [10, 0, 0], [ 0, 0,10],
          [ 0, 0, 0], [ 0, 0,10], [10, 0, 0],
          [ 0, 0, 0], [ 0,10, 0], [ 0, 0,10]];
polyhedron(points, [[0,1,2], [3,4,5], [6,7,8], [9,10,11], [12,13,14]]);

опишет тот же тетраэдр, что и: 

points = [[0,0,0], [0,10,0], [10,0,0], [0,0,10]];
polyhedron(points, [[0,2,1], [0,1,3], [1,2,3], [0,3,2]]);
Источник — https://ru.wikibooks.org/w/index.php?title=Руководство_пользователя_по_OpenSCAD/Язык_сценариев_OpenSCAD&oldid=211396