Руководство пользователя по OpenSCAD/Примитивы объемных тел
Куб
[править]cube() создает куб в первом октанте. Когда параметр center=true куб центрируется в начале координат.
Имена аргументов являются необязательными, если они заданы в указанном здесь порядке.
cube(size = [x,y,z], center = true/false); cube(size = x , center = true/false);
- Параметры :
- size
- одно значение, куб со всеми сторонами этой длины
- массив из 3-х значений [x, y, z], куб с размерами x, y и z.
- center
- false (по умолчанию), 1-й (положительный) октант, первый угол находится на (0,0,0)
- true, куб центрирован на (0,0,0)
- size
значения по умолчанию: cube(); выводит: cube(size = [1, 1, 1], center = false);
- примеры :
равнозначные описания для этого примера cube(size = 18); cube(18); cube([18,18,18]); . cube(18,false); cube([18,18,18],false); cube([18,18,18],center=false); cube(size = [18,18,18], center = false); cube(center = false,size = [18,18,18] );
равнозначные описания для этого примера cube([18,28,8],true); box=[18,28,8];cube(box,true);
Сфера
[править]Создает сферу в начале системы координат. Имя аргумента r является необязательным. Чтобы использовать d вместо r, d должен быть назван.
Параметры
- r
- Радиус. Это радиус сферы. Разрешение сферы зависит от размера сферы и переменных $fa, $fs и $fn. Для получения дополнительной информации об этих специальных переменных смотрите: OpenSCAD_User_Manual/Other_Language_Features
- d
- Диаметр. Это диаметр сферы.
- $fa
- Угол наклона фрагмента в градусах
- $fs
- Размер фрагмента в миллиметрах
- $fn
- Разрешение
значения по умолчанию: sphere(); выводит: sphere($fn = 0, $fa = 12, $fs = 2, r = 1);
Примеры использования
sphere(r = 1); sphere(r = 5); sphere(r = 10); sphere(d = 2); sphere(d = 10); sphere(d = 20);
// результатом будет сфера радиусом 2мм, с поверхностью высокого разрешения sphere(2, $fn=100);
// также создается сфера радиусом 2мм, с поверхностью высокого разрешения, но у этой // не так много маленьких треугольников на полюсах сферы sphere(2, $fa=5, $fs=0.1);
Цилиндр
[править]cylinder() создает цилиндр или конус с центром вокруг оси z. Если значение center равно true, оно также центрируется вертикально вдоль оси z.
Имена параметров являются необязательными, если они заданы в указанном здесь порядке. Если параметр получил имя, то все следующие параметры также должны быть поименованы.
ПРИМЕЧАНИЕ: Если используются r, d, d1 или d2, они должны быть названы.
cylinder(h = height, r1 = BottomRadius, r2 = TopRadius, center = true/false);
- Параметры
- h : высота цилиндра или конуса
- r : радиус цилиндра. r1 = r2 = r.
- r1 : радиус, нижней части конуса.
- r2 : радиус, верхней части конуса.
- d : диаметр цилиндра. r1 = r2 = d / 2. Шаблон:Требуется
- d1 : диаметр, нижней части конуса. r1 = d1 / 2. Шаблон:Требуется
- d2 : диаметр, верхней части конуса. r2 = d2 / 2. Шаблон:Требуется
- center
- false (по умолчанию), z в диапозоне от 0 до h
- true, z в диапозоне от -h/2 до +h/2
- $fa : минимальный угол (в градусах) каждого фрагмента.
- $fs : минимальная длина окружности каждого фрагмента.
- $fn : исправлено количество фрагментов в 360 градусах. Значения 3 или более переопределяют значения $fa и $fs
- $fa, $fs и $fn должны быть именованными параметрами. нажмите здесь для получения более подробной информации.
значения по умолчанию: cylinder(); выводит: cylinder($fn = 0, $fa = 12, $fs = 2, h = 1, r1 = 1, r2 = 1, center = false);
равнозначные описания для этого примера cylinder(h=15, r1=9.5, r2=19.5, center=false); cylinder( 15, 9.5, 19.5, false); cylinder( 15, 9.5, 19.5); cylinder( 15, 9.5, d2=39 ); cylinder( 15, d1=19, d2=39 ); cylinder( 15, d1=19, r2=19.5);
равнозначные описания для этого примера cylinder(h=15, r1=10, r2=0, center=true); cylinder( 15, 10, 0, true); cylinder(h=15, d1=20, d2=0, center=true);
-
center = false
-
center = true
равнозначные описания для этого примера cylinder(h=20, r=10, center=true); cylinder( 20, 10, 10,true); cylinder( 20, d=20, center=true); cylinder( 20,r1=10, d2=20, center=true); cylinder( 20,r1=10, d2=2*10, center=true);
- использование $fn
Большие значения $fn создают более гладкие, более круглые поверхности за счет увеличения времени рендеринга. Некоторые используют средние значения во время разработки для более быстрого рендеринга, а затем меняют значение на большое для окончательного рендеринга F6.
Однако использование малых значений может привести к появлению некоторых интересных некруглых объектов. Здесь показано несколько примеров:
описания для этих примеров cylinder(20,20,20,$fn=3); cylinder(20,20,00,$fn=4); cylinder(20,20,10,$fn=4);
- отверстия меньшего размера
Используя cylinder() с difference() для размещения отверстий в объектах, создаются отверстия меньшего размера. Это происходит потому, что круговые пути аппроксимируются многоугольниками, вписанными внутри круга. Точки многоугольника находятся на окружности, но прямые линии между ними находятся внутри. Чтобы все отверстия были больше истинного круга, многоугольник должен лежать полностью за пределами круга (описанного). Модули для описанных отверстий
описание для этого примера
poly_n = 6;
color("blue") translate([0, 0, 0.02]) linear_extrude(0.1) circle(10, $fn=poly_n);
color("green") translate([0, 0, 0.01]) linear_extrude(0.1) circle(10, $fn=360);
color("purple") linear_extrude(0.1) circle(10/cos(180/poly_n), $fn=poly_n);
Многогранник
[править]Многогранник - это наиболее общее трехмерное простейшее твердое тело. Его можно использовать для создания любой правильной или неправильной фигуры, в том числе с вогнутыми и выпуклыми частями. Изогнутые поверхности аппроксимируются несколькими плоскими поверхностями.
polyhedron( points = [ [X0, Y0, Z0], [X1, Y1, Z1], ... ], triangles = [ [P0, P1, P2], ... ], convexity = N); // до 2014.03 polyhedron( points = [ [X0, Y0, Z0], [X1, Y1, Z1], ... ], faces = [ [P0, P1, P2, P3, ...], ... ], convexity = N); // 2014.03 & позже
- Параметры
- points
- Вектор 3d точек или вершин. Каждая точка, в свою очередь, является вектором [x, y, z] своих координат.
- Точки могут быть определены в любом порядке. N точек указываются в определённом порядке, от 0 до N-1.
- points
- triangles Шаблон:OpenSCAD User Manual/Deprecated
- Вектор граней, которые в совокупности охватывают твердое тело. Каждая грань представляет собой вектор, содержащий индексы (на основе 0) 3 точек из вектора точек.
- faces Шаблон:Требует
- Вектор граней, которые в совокупности охватывают твердое тело. Каждая грань представляет собой вектор, содержащий индексы (на основе 0) 3 или более точек из вектора точек.
- Грани могут быть определены в любом порядке. Определите достаточное количество граней, чтобы полностью охватить твердое тело без перекрытия.
- Если точки, описывающие одну грань, не находятся в одной плоскости, грань автоматически разбивается на треугольники по мере необходимости.
- triangles Шаблон:OpenSCAD User Manual/Deprecated
- convexity
- Целое число. Параметр выпуклости указывает максимальное количество граней, через которые может пройти луч, пересекающий объект. Этот параметр необходим только для корректного отображения объекта в режиме предварительного просмотра OpenCSG. Это никак не влияет на рендеринг многогранника. При проблемах с отображением значение 10 должно работать нормально в большинстве случаев.
- convexity
значения по умолчанию: polyhedron(); выводит: polyhedron(points = undef, faces = undef, convexity = 1);
Вы можете начать с любой точки, но все грани должны иметь точки, расположенные в одном и том же направлении. OpenSCAD предпочитает по часовой стрелке, когда смотрит на каждую грань снаружи внутрь. Задняя часть просматривается сзади, нижняя часть снизу и т.д. Еще один способ запомнить это требование к порядку - использовать правило правой руки. Используя правую руку, поднимите большой палец вверх и согните пальцы, как бы показывая большой палец вверх, направьте большой палец в грань и расположите точки в направлении, в котором сгибаются ваши пальцы. Попробуйте сделать это на примере ниже.
- Пример 1 Использование многогранника для создания куба( [ 10, 7, 5 ] );
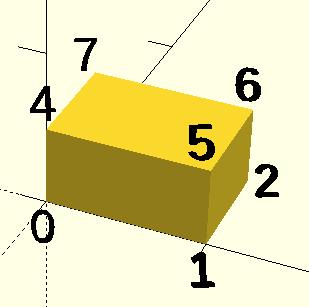
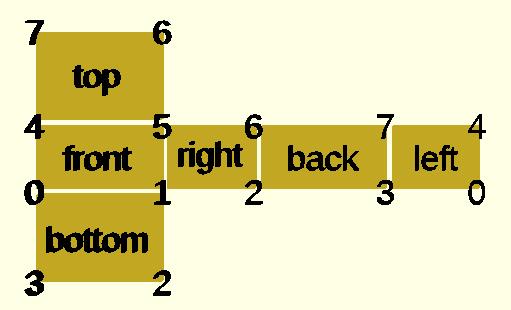
CubePoints = [ [ 0, 0, 0 ], //0 [ 10, 0, 0 ], //1 [ 10, 7, 0 ], //2 [ 0, 7, 0 ], //3 [ 0, 0, 5 ], //4 [ 10, 0, 5 ], //5 [ 10, 7, 5 ], //6 [ 0, 7, 5 ]]; //7 CubeFaces = [ [0,1,2,3], // bottom [4,5,1,0], // front [7,6,5,4], // top [5,6,2,1], // right [6,7,3,2], // back [7,4,0,3]]; // left polyhedron( CubePoints, CubeFaces );
равнозначные описания нижней грани [0,1,2,3], [0,1,2,3,0], [1,2,3,0], [2,3,0,1], [3,0,1,2], [0,1,2],[2,3,0], // 2 треугольника без перекрытия [1,2,3],[3,0,1], [1,2,3],[0,1,3],
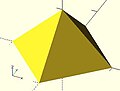
- Пример 2 Пирамида с квадратным основанием:

polyhedron(
points=[ [10,10,0],[10,-10,0],[-10,-10,0],[-10,10,0], // четыре точки в основании
[0,0,10] ], // точка вершины
faces=[ [0,1,4],[1,2,4],[2,3,4],[3,0,4], // все стороны треугольников
[1,0,3],[2,1,3] ] // два триугольника для квадратного основания
);
- Пример 3 Треугольная призма:

module prism(l, w, h){
polyhedron(
points=[[0,0,0], [l,0,0], [l,w,0], [0,w,0], [0,w,h], [l,w,h]],
faces=[[0,1,2,3],[5,4,3,2],[0,4,5,1],[0,3,4],[5,2,1]]
);
// предварительный просмотр развернутый (не включайте в свою функцию)
z = 0.08;
separation = 2;
border = .2;
translate([0,w+separation,0])
cube([l,w,z]);
translate([0,w+separation+w+border,0])
cube([l,h,z]);
translate([0,w+separation+w+border+h+border,0])
cube([l,sqrt(w*w+h*h),z]);
translate([l+border,w+separation+w+border+h+border,0])
polyhedron(
points=[[0,0,0],[h,0,0],[0,sqrt(w*w+h*h),0], [0,0,z],[h,0,z],[0,sqrt(w*w+h*h),z]],
faces=[[0,1,2], [3,5,4], [0,3,4,1], [1,4,5,2], [2,5,3,0]]
);
translate([0-border,w+separation+w+border+h+border,0])
polyhedron(
points=[[0,0,0],[0-h,0,0],[0,sqrt(w*w+h*h),0], [0,0,z],[0-h,0,z],[0,sqrt(w*w+h*h),z]],
faces=[[1,0,2],[5,3,4],[0,1,4,3],[1,2,5,4],[2,0,3,5]]
);
}
prism(10, 5, 3);
Отладка многогранников
[править]Ошибки при определении многогранников включают в себя отсутствие всех граней с одинаковым порядком, перекрытие граней и отсутствие граней или частей граней. Как правило, грани многогранника также должны удовлетворять нескольким условиям:
- ровно две грани должны встретиться на любом ребре многогранника.
- Если две грани имеют общую вершину, то они должны быть в в том же цикле грань-ребра вокруг вершины.
Первое правило исключает многогранники, такие как два куба с общим ребром, а не герметичные модели; второе исключает многогранники, такие как два куба с общей вершиной.
При взгляде снаружи точки, описывающие каждую грань, должны располагаться в одном и том же порядке. OpenSCAD предпочитает CW (clockwise - по Часовой Стрелке) и предоставляет механизм для обнаружения CCW (counterclockwise - Против Часовой Стрелки). Когда комбинированный вид (F12) используется с F5, грани ПЧС (CCW) отображаются розовым цветом. Измените порядок точек для неправильных граней. Поверните объект, чтобы просмотреть все грани. Розовый вид можно отключить с помощью F10.
OpenSCAD позволяет временно закомментировать часть описаний граней, чтобы отображались только оставшиеся грани. Используйте //, чтобы закомментировать остальную часть строки. Используйте /* и */, чтобы начать и закончить блок комментариев. Это может быть частью строки или распространяться на несколько строк. Просмотр только части граней может быть полезным при определении правильных точек для отдельной грани. Обратите внимание, что твердое тело не отображается, только грани. При использовании F12 все грани имеют одну розовую сторону. Комментирование некоторых граней помогает также показать любое внутреннюю грань.

CubeFaces = [ /* [0,1,2,3], // bottom [4,5,1,0], // front */ [7,6,5,4], // top /* [5,6,2,1], // right [6,7,3,2], // back */ [7,4,0,3]]; // left
После определения многогранника его предварительный просмотр может показаться правильным. Один только многогранник может даже хорошо отрисоваться. Однако, чтобы убедиться, что это допустимое множество и что оно может генерировать допустимый файл STL, объедините его с любым кубом и визуализируйте его (F6). Если многогранник исчезает, это означает, что он неправильный. Пересмотрите порядок намотки всех граней и два правила, изложенные выше.
Неправильно направленные грани
[править]- Пример 4 более сложный многогранник с неправильно упорядоченными гранями
Если вы выберете 'Всё вместе (Thrown together) [F12]' в меню Вид (View) и скомпилируйте дизайн [F5] (не компелировать и рендер! [F6]) предварительный просмотр покажет выделением неправильно направленные полигоны. К сожалению, это выделение невозможно в режиме предварительного просмотра OpenCSG, поскольку это помешало бы реализации режима предварительного просмотра OpenCSG.
Ниже вы можете увидеть код и изображение такого проблемного многогранника, плохие полигоны (грани или сочетания граней) окрашены в розовый цвет.
// Плохой многогранник
polyhedron
(points = [
[0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60],
[10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
],
faces = [
[0,2,3], [0,1,2], [0,4,5], [0,5,1], [5,4,2], [2,4,3],
[6,8,9], [6,7,8], [6,10,11], [6,11,7], [10,8,11],
[10,9,8], [0,3,9], [9,0,6], [10,6, 0], [0,4,10],
[3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,7,8],
[1,8,2], [2,8,11], [2,11,5]
]
);

Правильный многогранник был бы следующим:
polyhedron
(points = [
[0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60],
[10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
],
faces = [
[0,3,2], [0,2,1], [4,0,5], [5,0,1], [5,2,4], [4,2,3],
[6,8,9], [6,7,8], [6,10,11],[6,11,7], [10,8,11],
[10,9,8], [3,0,9], [9,0,6], [10,6, 0],[0,4,10],
[3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,8,7],
[2,8,1], [8,2,11], [5,11,2]
]
);
- Совет для начинающих
Если вы действительно не понимаете "ориентацию", попробуйте определить неправильно ориентированные розовые грани, а затем перевернуть последовательность ссылок на векторы точек, пока не получите правильное отображение. К примеру, в приведенном выше примере третий треугольник([0,4,5]) был неправильным, и мы исправили это так [4,0,5]. Помните, что список граней - это круговой список. Кроме того, вы можете выбрать "Показать ребра" в меню "Вид", распечатать снимок экрана и пронумеровать как точки, так и грани. В нашем примере точки помечены черным цветом, а грани - синим. Переверните объект и при необходимости сделайте вторую копию с обратной стороны. Таким путём вы сможете держать верное направление (This way you can keep track).
- Техника по часовой стрелке
Ориентация определяется круговым указанием по часовой стрелке. Это означает, что если вы смотрите на треугольник (в этом случае [4,0,5]) снаружи вы увидите, что путь проходит по часовой стрелке вокруг центра грани. Порядок намотки [4,0,5] по часовой стрелке и, следовательно, хорошо. Порядок намотки [0,4,5] против часовой стрелки и, следовательно, плохо. Аналогично, любой другой порядок по часовой стрелке [4,0,5] работает: [5,4,0] и [0,5,4] тоже хорошо. Если вы используете технику по часовой стрелке, ваши грани всегда будут снаружи (за пределами OpenSCAD, хотя другие программы используют против часовой стрелки в качестве внешней стороны).
Думайте об этом как о Правиле Левой Руки:
Если вы положите левую руку на грань, согнув пальцы в направлении порядка точек, ваш большой палец должен быть направлен наружу. Если ваш большой палец указывает внутрь, вам нужно изменить порядок намотки.

Краткое описание 'Многогранника'
* Точки определяют все точки/вершины фигуры. * Грани - это список плоских многоугольников, соединяющих точки/вершины.
Каждая точка в списке точек определяется с помощью 3-мерной x,y,z характеристики положения. Точки в списке точек автоматически перечисляются, начиная с нуля, для использования в списке граней (0,1,2,3,... и т.д.).
Каждая грань в списке граней определяется путем выбора 3 или более точек (с использованием порядкового номера точек) из списка точек.
например, faces=[ [0,1,2] ] определяет треугольник из первой точки (точки равны нулю) ко второй точке, а затем к третьей точке.
При взгляде на любую грань снаружи, на ней должны быть перечислены все точки в порядке по часовой стрелке.
Повторения точек в списке точек многогранника
[править]Список точек определения многогранника может содержать повторы. Когда две или более точки имеют одинаковые координаты, они считаются одной и той же вершиной многогранника. Итак, следующий многогранник:
points = [[ 0, 0, 0], [10, 0, 0], [ 0,10, 0],
[ 0, 0, 0], [10, 0, 0], [ 0,10, 0],
[ 0,10, 0], [10, 0, 0], [ 0, 0,10],
[ 0, 0, 0], [ 0, 0,10], [10, 0, 0],
[ 0, 0, 0], [ 0,10, 0], [ 0, 0,10]];
polyhedron(points, [[0,1,2], [3,4,5], [6,7,8], [9,10,11], [12,13,14]]);
опишет тот же тетраэдр, что и:
points = [[0,0,0], [0,10,0], [10,0,0], [0,0,10]];
polyhedron(points, [[0,2,1], [0,1,3], [1,2,3], [0,3,2]]);