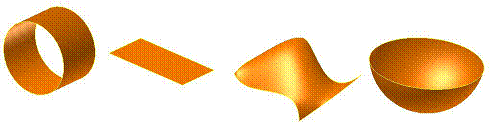Autodesk Inventor API. Первые шаги/TransientGeometry
Что такое Transient Geometry?
[править]Вспомогательная геометрия (transient geometry) предназначена для решения через API комплекса математических задач, преимущественно геометрических. Объекты вспомогательной геометрии создаются посредством вызовов соответствующих методов объекта TransientGeometry и чрезвычайно широко используются в Autodesk Inventor API. В отличие от большинства других геометрических объектов API, эти объекты не имеют средств визуального отображения. Чаще всего, это абстрактные математические объекты–посредники, предназначенные для управления объектами «реальной» геометрии Autodesk Inventor. Например, математические 2D и 3D точки TransientGeometry используются для создания и манипуляции рабочими и эскизными точками, построения матриц преобразований и многого другого.
Слово «transient» (временный) подчеркивает короткоживущий характер этих объектов. Срок их жизни ограничен одним сеансом работы Инвентора, и в файлах они не сохраняются.
В Inventor 2008 API в составе TransientGeometry разработчиками предусмотрены три группы объектов:
- геометрические (Geometry),
- математические (Math) и
- вспомогательные (Utility).
Группа геометрических объектов выглядит следующим образом:
На следующем рисунке приведены группы математических и вспомогательных объектов.
В группе Utility заслуживают внимания объекты для поддержки коллекций ребер EdgeCollection, граней FaceCollection и произвольных объектов ObjectCollection.
Объекты вспомогательной геометрии представляют собой математические абстракции реальных геометрических объектов и лишены многих их свойств. Например, объект Line, в отличие, скажем, от эскизной линии SketchLine, имеет бесконечную длину. Line имеет выделенное направление Direction, заданное её единичным вектором типа UnitVector. Аналогично и объект Plane отличается от плоской грани отсутствием пространственных границ. В отличие от геометрической плоскости, известной нам из школьного курса математики, объект Plane имеет выделенное направление — это направление вектора нормали к плоскости Normal, заданное единичным вектором типа UnitVector. Именно это обстоятельство позволяет отличать одну сторону плоскости от другой.
Существенной особенностью объектов вспомогательной геометрии является их неассоциативный характер. Извлекаемая из объекта-entity геометрия точно отражает геометрию "родителя" в момент рождения, но ассоциативной связи с ним не имеет. Так, возвращаемый ребром объект LineSegment точно описывает его начальную и конечную точки. Но если родительское ребро будет изменено (скажем, вы увеличите длину выдавливания), то полученный до изменений вспомогательный геометрический объект LineSegment актуальным быть уже перестанет — он ничего «не знает» о последующей эволюции ребра-родителя, поскольку представляет своего рода «мгновенный снимок» геометрии родительского ребра в момент своего рождения. Созданные объекты вспомогательной геометрии можно модифицировать. Например, можно передвинуть начальную и конечную точки, однако это не приведет к изменениям в родительской геометрии объекта-entity, т.к. связь между ним разрывается с момента рождения объекта вспомогательной геометрии.
Объект TransientGeometry, доступ к которому обеспечивает одноименное свойство объекта Application, позволяет также создавать объекты вспомогательной геометрии и непосредственно — без привлечения родительских объектов-entity. Например, метод CreateLineSegment служит для создания объекта LineSegment на базе начальной и конечной точек. С точки зрения конечного пользователя в Инвенторе ровным счетом ничего не происходит. Вы не увидите в графическом окне новой линии. Если вы сохраните текущий документ, этот линейный сегмент сохранен не будет. То, что вы создали, является лишь абстрактным геометрическим описанием линейного сегмента, но не «настоящей» линией-entity.
Точки (Points)
[править]В Инвенторе имеются несколько объектов-entity, которые представляют точки:
- вершина (vertex),
- рабочая точка (work point),
- точка в 3D-эскизе (3D sketch point) и
- точка в 2D-эскизе (2D sketch point).
Первые три всегда задают 3D-точку в пространстве модели. Двумерная эскизная точка описывает 2D-точку в пространстве координат плоского эскиза. Из любого из перечисленных объектов можно извлечь геометрическую точку как объект вспомогательной геометрии. Трехмерные объекты возвращают объект Point, точка 2D-эскиза возвращает объект Point2d. Геометрическая точка обеспечивает доступ к своим координатам (x,y,z) или (x,y), соответственно.
Вместо объекта Point для задания геометрической точки вполне можно было бы применять массив из трех действительных чисел. Однако точка как объект Point не только хранит в себе данные о координатах, но, что вероятно самое важное, она поддерживает дополнительные функции, которые очень полезны при манипуляциях с точками. Например, в дополнение к возможности считывать и задавать координаты точки (x,y,z) объект Point поддерживает метод DistanceTo, который возвращает расстояние до другой точки. Имеются еще несколько полезных методов, которые делают объект Point гораздо более удобным в работе, нежели массив из трех координат.
Точки Point и Point2d
[править]Объект Point описывает трехмерную математическую точку в декартовом пространстве на основе списка из трех ее координат X, Y и Z. Его двумерный аналог — объект Point2d — представляет собой математическую точку с координатами X и Y на плоскости. Оба объекта обеспечивают доступ к координатам и поддерживают ряд методов для проверки эквивалентности и геометрических преобразований.
Точки Point2d широко применяются при работе в двумерными эскизами. Чтобы создать в эскизе эскизную точку SketchPoint, используется метод Add коллекции эскизных точек SketchPoints. Методу Add требуется знать положение, в котором следует создавать эскизную точку SketchPoint. Но эта точка может быть результатом произвольной последовательности преобразований и перемещений, или может быть точкой другого объекта. По этой причине метод Add опирается на объект Point2d.
' Поскольку пример демонстрационный,
' то с целью упрощения опущена проверка ошибок.
' Всегда проверяйте корректность типа возвращаемых значений.
Dim oApp As Inventor.Application
Set oApp = ThisApplication
Dim oPartDoc As PartDocument
Set oPartDoc = oApp.Documents.Add( _
kPartDocumentObject, _
oApp.GetTemplateFile(kPartDocumentObject))
' Создаем эскиз в плоскости XY
Dim oSketch As PlanarSketch
Set oSketch = oPartDoc.ComponentDefinition.Sketches.Add _
(oPartDoc.ComponentDefinition.WorkPlanes.Item(3))
Dim oTG As TransientGeometry
Set oTG = oApp.TransientGeometry
Dim oSkPnts As SketchPoints
Set oSkPnts = oSketch.SketchPoints
Call oSkPnts.Add(oTG.CreatePoint2d(30, 20), False)
Приведенный фрагмент программы создает эскиз с единственной эскизной точкой с координатами X=30, Y=20. Последний аргумент метода Add является логическим значением, которое определяет, является ли создаваемая эскизная точка центром отверстия. Но это влияет лишь на ее графическое отображение.
Эскизные точки в коллекции SketchPoints всегда двумерные, имеют тип SketchPoint. Методу Add для их создания требуется предоставить объект Point2d, для чего обычно применяется метод CreatePoint2D.
Трехмерные эскизные точки типа SketchPoint3D хранятся в другой коллекции SketchPoints3D.
Кривые (Curves)
[править]В общем случае кривые являются обобщением линий произвольной геометрии: сплайнов, окружностей, дуг, прямых линий и т.д. Инвентор поддерживает множество 2- и 3-мерных объектов-entity, таких как ребро Edge, эскизная линия SketchLine, эскизная дуга SketchArc, рабочая ось WorkAxis, эскизный сплайн SketchSpline и т.д. Из каждого такого объекта можно извлечь геометрический объект который предоставит информацию о форме родительского объекта-entity. Примерами таких геометрических объектов являются объекты LineSegment, BSplineCurve, Circle, Arc и др.
Рассмотрим пример выяснения геометрии выделенного пользователем ребра.
Public Sub CurveGeometry()
' Ссылка на активный документ
Dim oPartDoc As PartDocument
Set oPartDoc = ThisApplication.ActiveDocument
' Ссылка на выделенное ребро
On Error Resume Next
Dim oEdge As Edge
Set oEdge = oPartDoc.SelectSet.Item(1)
If Err Then
MsgBox "Следует выделить ребро."
Exit Sub
End If
On Error GoTo 0
End Sub
Тип геометрии многих объектов-entity в силу их специфики известен заранее. Например, SketchLine всегда возвращает объект LineSegment2d, а SketchLine3D — LineSegment, тогда как SketchCircle3D обязательно вернет объект Circle. Объект Edge в этом отношении уникален, поскольку может иметь различную форму. Это означает, что тип возвращаемого им объекта вспомогательной геометрии зависит от геометрической формы ребра. Приведенный ниже фрагмент кода дополняет предыдущий пример уточнением типа ребра с помощью проверки его свойства CurveType, после чего печатается соответствующая геометрическая информация.
' Проверка типа геометрии и вывод ее специфических параметров
Select Case oEdge.GeometryType
Case kLineSegmentCurve
Dim oLineSegment As LineSegment
Set oLineSegment = oEdge.Geometry
Debug.Print "Начальная точка: " & PointString(oLineSegment.StartPoint)
Debug.Print "Конечная точка: " & PointString(oLineSegment.EndPoint)
Case kCircleCurve
Dim oCircle As Inventor.Circle
Set oCircle = oEdge.Geometry
Debug.Print "Центр: " & PointString(oCircle.Center)
Debug.Print "Радиус: " & Format(oCircle.Radius, "0.0000")
Case kCircularArcCurve
Dim dPi As Double
dPi = Atn(1) * 4
Dim oArc As Inventor.Arc3d
Set oArc = oEdge.Geometry
Debug.Print "Центр: " & PointString(oArc.Center)
Debug.Print "Радиус: " & Format(oArc.Radius, "0.0000")
Debug.Print "Угол: " & Format(oArc.SweepAngle * (180 / dPi), "0.0000")
Case Else
Debug.Print "Геометрия выделенного объекта не поддерживается."
End Select
End Sub
Private Function PointString(PointOrVector As Object) As String
' Для заданного аргументом вектора или точки
' возвращает строку с координатами X,Y,Z
PointString = Format(PointOrVector.X, "0.0000") & "," & _
Format(PointOrVector.Y, "0.0000") & "," & _
Format(PointOrVector.Z, "0.0000")
End Function
Дополнительную информацию о кривой можно получить с помощью объекта CurveEvaluator. Этот объект вспомогательной геометрии можно извлечь из любой кривой, в том числе и из ребра Edge. Подход к анализу геометрии с помощью объекта CurveEvaluator имеет общий характер и применим к любым видам геометрии. Для извлечения пользы из объекта CurveEvaluator важно понять концепцию параметрического пространства. В случае кривой это будет параметрическое пространство данной кривой. Если поставить числовую ось в соответствие кривой, любую точку на кривой можно задать всего одним числом. На рисунке ниже эта идея проиллюстрирована на примере ребра. Параметрическое пространство этой кривой имеет диапазон от 0 до 2,54. На ребре показана серия точек, положение на ребре любой из них может быть поставлено в соответствие конкретному значению параметра в параметрическом пространстве ребра.
Этот подход применим к ребрам любой формы. Ниже показано параметрические пространства рёбер в форме сплайна и окружности. Как видно из этих трех примеров, диапазон изменения параметра для разных кривых может отличаться. В первом случае параметр изменялся в диапазоне от 0 до 2,54, во втором — от –1 до 0, в третьем —
от до .
Понимание идеи параметрического пространства является критически важным для полноценного использования функционала объекта CurveEvaluator. Большинство его методов либо используют параметры как входные аргументы, либо возвращают их в качестве результата.
Вот список наиболее часто применяемых методов объекта CurveEvaluator.
- GetParamExtents — возвращает границы диапазона изменения параметра данной кривой.
- GetPointAtParam — по значению параметра определяет точку на кривой в пространстве модели.
- GetParamAtPoint — вычисляет значение параметра для заданной точки на кривой.
- GetLengthAtParam — вычисляет длину между точками кривой, которые соответствуют двум заданным значениям параметра. Если в качестве входных аргументов задать минимальное и максимальное значения параметра, метод вернет полную длину кривой.
- GetParamAtLength — вычисляет значение параметра в точке, удаленной от другой параметрической точки на заданное расстояние вдоль кривой.
- GetTangent — возвращает вектор касательной к кривой в точке, заданной параметром.
- GetCurvature — вычисляет кривизну в точке, заданной параметром.
Код следующего примера иллюстрирует технику работы с параметрическим пространством кривой. Используются методы GetParamExtents и GetPointAtParam.
' Ссылка на решатель кривой
Dim oCurveEval As CurveEvaluator
Set oCurveEval = oEdge.Evaluator
' Вычисление границ диапазона пространства параметров
Dim dMinParam As Double
Dim dMaxParam As Double
Call oCurveEval.GetParamExtents(dMinParam, dMaxParam)
' Ссылка на вспомогательную геометрию приложения
Dim oTG As TransientGeometry
Set oTG = ThisApplication.TransientGeometry
' В 11 равноотстоящих точках на кривой вычисляет и
' печатает соответствующие им значения параметра.
Dim i As Integer
For i = 0 To 10
' Значение параметра в точке i
Dim currentParam As Double
currentParam = dMinParam + ((dMaxParam - dMinParam) / 10) * i
' значение параметра сохраняется в массиве, т.к. метод GetPointAtParam
' использует в качестве аргумента только массив типа Double.
Dim adParam(0) As Double
adParam(0) = currentParam
' Вычисление координат в пространстве модели,
' соответствующих заданной параметрической точке
Dim adPoints(2) As Double
Call oCurveEval.GetPointAtParam(adParam, adPoints)
' печать результатов
Debug.Print "Параметр : " & Format(currentParam, "0.0000") & _
"Координаты: " & Format(adPoints(0), "0.000000") & "," & _
Format(adPoints(1), "0.000000") & "," & _
Format(adPoints(2), "0.000000")
Next i
End Sub
Поверхности (Surfaces)
[править]Поверхности в Инвенторе встречаются как в твердотельных, так и в поверхностных моделях. Во многих случаях и рабочие плоскости могут рассматриваться как поверхности. Описание поверхностей во многом сходно с описанием кривых и даже в чем-то проще, поскольку поверхности существуют только в трехмерном пространстве, и единственными объектами, имеющими поверхности, являются грани (Face) и рабочие плоскости (WorkPlane).
Как и в случае кривых, вы получаете вспомогательную геометрию из объекта-entity и используете ее данные для выяснения геометрической формы родительского объекта. Объект WorkPlane в качестве своей геометрии всегда возвращает плоскость. Объекты Face в зависимости от формы грани могут возвращать геометрию в виде объектов нескольких типов. Для выяснения типа геометрии, возвращаемой свойством Face.Geometry, следует использовать свойство SurfaceType объекта Face. Ниже приведен пример определения типа выделенной грани.
Public Sub SurfaceGeometry()
' Ссылка на активный документ
Dim oPartDoc As PartDocument
Set oPartDoc = ThisApplication.ActiveDocument
' Ссылка на выделенную грань
On Error Resume Next
Dim oFace As Face
Set oFace = oPartDoc.SelectSet.Item(1)
If Err Then
MsgBox "Следует выделить грань."
Exit Sub
End If
On Error GoTo 0
' Выяснение типа геометрии грани и печать её параметров.
Select Case oFace.SurfaceType
Case kPlaneSurface
Dim oPlane As Plane
Set oPlane = oFace.Geometry
Debug.Print "Planar face"
Debug.Print " Базовая точка : " & PointString(oPlane.RootPoint)
Debug.Print " Вектор нормали: " & PointString(oPlane.Normal)
Case kCylinderSurface
Dim oCylinder As Cylinder
Set oCylinder = oFace.Geometry
Debug.Print "Cylindrical face"
Debug.Print " Базовая точка: " & PointString(oCylinder.BasePoint)
Debug.Print " Воктор оси : " & PointString(oCylinder.AxisVector)
Debug.Print " Радиус : " & Format(oCylinder.Radius, "0.000000")
Case kSphereSurface
Dim oSphere As Sphere
Set oSphere = oFace.Geometry
Debug.Print "Spherical face"
Debug.Print " Центр : " & PointString(oSphere.CenterPoint)
Debug.Print " Радиус: " & Format(oSphere.Radius, "0.000000")
Case Else
Debug.Print "Этот тип геометрии не поддерживается: " & _
TypeName(oFace.Geometry)
End Select
End Sub
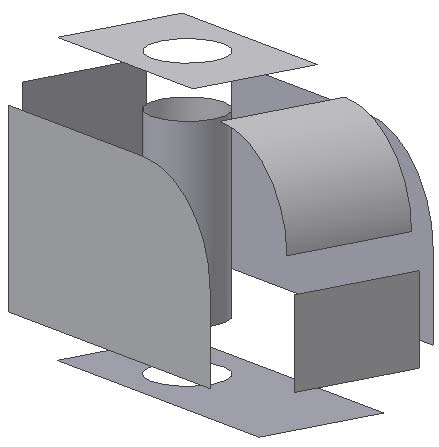
Важно отметить, что большинство поверхностных объектов вспомогательной геометрии границ не имеют. Например, плоскость задана только базовой точкой и вектором нормали и бесконечна в пространстве. Цилиндр задан началом координат, осью и радиусом, но длины не имеет. На следующем рисунке показано цилиндрическое тело, которое вполне может существовать в Инвенторе. Вполне очевидно, что цилиндр этот отнюдь не является неограниченным по длине и, более того, имеет отверстия и неровные кромки. Такое может быть в Инвенторе, т.к. рёбра определяются не поверхностью цилиндра, а рёбрами грани, которые и определяют ее границы. Это справедливо для поверхностей любого типа.
Поверхности, как и кривые, также имеют пространство параметров. Однако в отличие от кривых, параметрическое пространство поверхности является двумерным. Два параметрических значения определяют любую координатную точку на поверхности. Проще всего это продемонстрировать на примере плоского прямоугольника. На рисунке ниже приведен прямоугольный фрагмент плоскости с нанесенной координатной сеткой, иллюстрирующей параметрическое пространство поверхности, очень похожее на обычную двумерную координатную систему. Вы можете определить любую точку на плоскости, задав пару координат X и Y. В параметрическом пространстве аналогами координат X и Y являются переменные U и V.
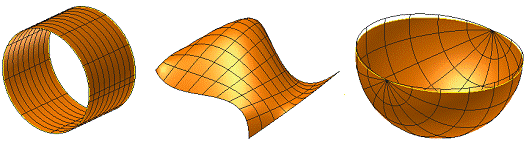
Ниже показаны примеры поверхностей с нанесенной параметрической сеткой. Несмотря на то, что поверхности не являются плоскими, вы по-прежнему можете любую точку поверхности задать парой координат U-V.
Как и в случае кривых, поверхности также поддерживают решатели. Объект SurfaceEvaluator можно получить либо из объекта Face, либо из любого другого объекта, описывающего поверхность. В общем случае желательно использовать решатель объекта Face, поскольку он учитывает дополнительную информацию, извлекаемую из модели твердого тела. Например, при вычислении вектора нормали к грани тела он всегда возвращает направление наружу. Объект SurfaceEvaluator по функциональности близок к CurveEvalutor. Вот список наиболее часто применяемых его методов и свойств.
- ParamRangeRect — возвращает границы диапазона изменения параметров u-v поверхности.
- GetPointAtParam — для пары значений параметров u-v возвращает в пространстве модели точку на поверхности.
- GetParamAtPoint — для заданной в пространстве модели точки на поверхности возвращает пару значений u-v в пространстве параметров.
- IsParamOnFace — свойство определяет, соответствует ли параметрическим координатам u-v реальная точка на поверхности грани или нет. Это особенно полезно, если в грани имеются, скажем, отверстия.
- GetNormal — возвращает вектор нормали к поверхности в точке, заданной параметрическими координатами u-v.
Ниже приведен небольшой пример использования этих функций для вычисления вектора нормали к выделенной грани. Использованная в программе точка грани является центром ее параметрического пространства. Способ получения ссылки на выделенную грань был рассмотрен в предыдущем примере.
' ссылка на решатель грани.
Dim oSurfEval As SurfaceEvaluator
Set oSurfEval = oFace.Evaluator
' определение диапазонов изменения параметров.
Dim oParamRange As Box2d
Set oParamRange = oSurfEval.ParamRangeRect
' вычисление параметрических координат u-v в центре поверхности.
' (Этот фрагмент чуть больше, чем мог бы быть, чтобы обойти проблему в VBA.)
Dim adParamCenter(1) As Double
Dim U As Double, V As Double
U = oParamRange.MinPoint.X
V = oParamRange.MaxPoint.X
adParamCenter(0) = (U + V) / 2
U = oParamRange.MinPoint.X
V = oParamRange.MaxPoint.X
adParamCenter(1) = (U + V) / 2
' Вычисление вектора нормали в точке u-v.
Dim adNormal(2) As Double
Call oSurfEval.GetNormal(adParamCenter, adNormal)
' Вывод координат вектора нормали.
Debug.Print "Нормаль: " & Format(adNormal(0), "0.000000") & "," & _
Format(adNormal(1), "0.000000") & "," & _
Format(adNormal(2), "0.000000")
' Вычисление точки в пространстве модели,
' в которой вычислен вектор нормали к грани.
Dim adPoint(2) As Double
Call oSurfEval.GetPointAtParam(adParamCenter, adPoint)
' Print the coordinate.
Debug.Print "Точка начала вектора нормали: " & _
Format(adPoint(0), "0.000000") & "," & _
Format(adPoint(1), "0.000000") & "," & _
Format(adPoint(2), "0.000000")
End Sub
Твердые тела (Solids)
[править]Типичные детали представлены в Инвенторе твердыми телами. Твердое тело лежит в основе интуитивно понятного и естественного способа работы с геометрией, поскольку является аналогом доступного для манипуляций объекта реального мира. В Инвенторе твердое тело создается и изменяется посредством конструктивных элементов, которые удаляют либо добавляют в тело материал. Поскольку Инвентор является параметрическим ассоциативным моделлером, вы можете редактировать модель, изменяя те или иные независимые параметры конструктивных элементов с последующим перевычислением модели.
С точки зрения Инвентора конструктивные элементы представляют собой наборы команд. В результате выполнения предписанной последовательности команд Инвентор создает или изменяет модель твердого тела. Данная статья фокусируется не на внутренних процессах, приводящих к созданию модели, а на твердотельной модели как конечном результате этих операций и инструментарии API для работы с ней.
Твердое тело в Инвенторе представлено описанием границ этого тела (Boundary Representation, B-Rep). Структура данных B-Rep является описанием совокупности связанных поверхностей, формирующих внешнюю границу объема тела. И хотя модель представляется нам твердотельной (мы можем что-нибудь из нее вырезать, определить весовые характеристики, проводить расчеты и иные характерные для твердых тел операции), в действительности это лишь набор поверхностей. Связность поверхностей относится к области топологии, и в модели B-Rep для этих задач предусмотрены необходимые инструменты. На рисунке ниже приведена простая модель твердого тела, которая будет использована для иллюстрации этих концепций.
С точки зрения API твердое тело описывается объектом SurfaceBody. Несмотря на то, что в его имени присутствует слово «поверхность» (“Surface”), объект SurfaceBody является обобщенным объектом, представляющим любой высокоуровневый объект B-Rep, включая и твердые, и поверхностные тела. Основное отличие твердотельной модели заключается в том, что она формируется замкнутой совокупностью поверхностей. Каждая ограничивающая тело поверхность в объекте SurfaceBody представлена объектом Face (грань). Как видно из следующего рисунка, в нашем примере границы тела сформированы восемью гранями. Объект Face поддерживает грани произвольной геометрии, независимо от их формы. Предыдущее обсуждение поверхностей касалось вопросов доступа к информации о геометрии грани.
Для формирования твердотельной модели недостаточно иметь ограничивающие тело поверхности. Важно, чтобы они были связанными между собой. Контакт между гранями описывается объектом Edge (ребро) и геометрически представлен некоторой кривой. Каждая грань «знает» ограничивающие ее ребра, и каждое ребро «знает», какие две грани оно соединяет. Другим полезным для программиста элементом топологии являются замкнутые контуры (loop). В объектной модели API они представлены объектом EdgeLoop. В общем случае замкнутый контур формируется группой последовательно соединенных ребер. На рисунке ниже одна грань имеет границы в виде двух замкнутых контуров. Внутренний контур в центре грани сформирован из одного круглого ребра. Внешний контур состоит из четырех прямолинейных рёбер. Замкнутые контуры образуют границы граней.
Другим распространенным объектом B-Rep является объект Vertex (вершина). Вершины существуют на концах любого ребра и описывают точки контакта между ребрами. Всякое ребро «знает» вершины на своих концах, и всякая вершина «знает», какие ребра в этой вершине соединены.
Еще одним, хотя и не слишком часто применяемым объектом B-Rep, является FaceShell. В Инвенторе вполне возможна ситуация, когда тело (solid) оказывается состоящим более, чем из одной части. Пример такого тела приведен на следующем рисунке . Тело слева состоит из одной части. Справа то же тело разделилось на две части в результате увеличения диаметра центрального отверстия. Несмотря на то, что визуально модель оказалась разделенной надвое, с точки зрения API она по-прежнему остается моделью одного тела и представлена одним объектом SurfaceBody. Однако каждый «осколок» представлен своим собственным объектом FaceShell. Большинство деталей имеют лишь один объект FaceShell, но, как видим, их может быть и больше. Другим примером может служить полый шар, сформированный двумя концентрическими сферическими поверхностями. В целом шар является одним телом и представлен одним объектом SurfaceBody, но внешняя и внутренняя сферические поверхности имеют свои собственные объекты FaceShell. Если в таком шаре просверлить отверстие, которое соединит внешнюю и внутреннюю сферы, то грани объединятся, и останется только один объект FaceShell.
Векторы (Vector)
[править]Вектор предоставляет удобный способ задания направления и величины. 3D-вектор имеет три компоненты x,y,z, а 2D-вектор — только две, x и y. Несмотря на простоту, объект Vector поддерживает богатый набор методов и свойств, которые облегчают векторные операции. Рассмотрим пару примеров с векторами. Весьма распространенным применением векторов является задание направления и величины перемещения объектов. Операция перемещения (трансляция) объекта в пространстве не предполагает вращения объекта. Например, вектор (3,1,0) определяет перемещение объекта на 3 единицы вдоль оси X, на 1 единицу вдоль оси Y и 0 единиц вдоль оси Z, что приводит к смещению объекта на расстояние 3.162 единиц, как показано ниже.
Другой распространенной задачей векторов является задание направлений. В предыдущем примере вектор использовался для задания и направления и величины перемещения детали. В случаях, когда требуется задать лишь направление, обычно используются единичные векторы в виде объектов типа UnitVector. Длина вектора UnitVector всегда равна единице. Примером, когда векторы используются для задания направлений, является получение от некоторых объектов вспомогательной геометрии данных об ориентации. Например, объект Cylinder (Цилиндр) поддерживает свойство AxisVector (вектор оси), которое возвращает единичный вектор типа UnitVector. Он описывает направление в пространстве оси цилиндра.
Функционал объекта Vector определяется набором его методов и свойств. Рассмотрим наиболее употребительные из них. При определении прямоугольной системы координат вы обычно имеете точку, которая станет началом системы координат (Origin), и три вектора, которые задают направления осей x, y и z. Ими могут быть и единичные векторы, поскольку их длины значения не имеют. Чтобы система координат была действительно прямоугольной, векторы должны удовлетворять следующим условиям:
- Направление оси y должно быть перпендикулярно направлению оси x.
- Направление оси z должно быть перпендикулярно направлениям осей x и y, а также удовлетворять правилу правой руки, т.к. в Инвенторе используются только правые системы координат.
Рассмотрим на конкретном примере простой метод создания трех векторов, одновременно удовлетворяющих перечисленным условиям. Предположим, требуется задать координатную систему, в которой ось x направлена вдоль направления (3, 7, 6), ось y должна быть направлена вверх, это будет её положительное направление. И наконец, ось z должна быть корректно сориентирована относительно осей x и y.
Для векторов определена операция, называемая векторным произведением, которая по двум неколлинеарным векторам позволяет вычислить третий вектор. Любые два непараллельных вектора задают плоскость. Если вы совместите начала двух таких векторов, они будут лежать в одной плоскости. Результатом векторного произведения этих векторов является третий вектор, перпендикулярный этой плоскости (см. рисунок справа). Направление вектора z зависит от последовательности векторов x и y в операции векторного произведения. Вектор z, показанный на рисунке, является результатом векторного произведения вектора x на вектор y и удовлетворяет правилу правой руки. Направьте указательный палец правой руки вдоль оси x, а средний палец влево вдоль оси y, тогда направленный вверх большой палец правой руки укажет положительное направление вектора z. Если в векторном произведении векторы x и y поменять местами, то направление результирующего вектора z изменится на противоположное.
Посмотрим, как с помощью векторного произведения можно построить описанную в задаче систему координат. Сначала пошагово опишем алгоритм, а затем рассмотрим его программную реализацию.
- Создать вектор в известном направлении оси x, (3,7,6).
- Создать вектор который определяет ось y, направление (0,1,0). (Понятно, что это не точное направление оси y, а лишь его грубое приближение.)
- Вычислить вектор z как векторное произведение вектора x на вектор y. Полученное направление является точным (это направление нормали к плоскости, в которой лежат векторы x и y).
- Вычислить вектор y как векторное произведение вектора z на вектор x. Полученное направление вектора y является точным.
Public Sub CreateCoordSystem() ' Ссылка на вспомогательную геометрию. Dim oTG As TransientGeometry Set oTG = ThisApplication.TransientGeometry ' создание вектора для оси x. Dim oXAxis As UnitVector Set oXAxis = oTG.CreateUnitVector(3, 7, 6) ' создание первого приближения для вектора в направлении оси y. Dim oYAxis As UnitVector Set oYAxis = oTG.CreateUnitVector(0, 1, 0) ' Вычисление вектора z как векторного произведения x на y. Dim oZAxis As UnitVector Set oZAxis = oXAxis.CrossProduct(oYAxis) ' Создание вектора y как векторного произведения z на x. Set oYAxis = oZAxis.CrossProduct(oXAxis) ' Вывод результатов Debug.Print "Ось x: " & oXAxis.X & ", " & oXAxis.Y & ", " & oXAxis.Z Debug.Print "Ось y: " & oYAxis.X & ", " & oYAxis.Y & ", " & oYAxis.Z Debug.Print "Ось z: " & oZAxis.X & ", " & oZAxis.Y & ", " & oZAxis.Z End Sub
Пару слов стоит сказать и о других функциях, поддерживаемых объектом Vector. Методы AngleTo, IsEqualTo, IsParallelTo и IsPerpendicularTo позволяют различными способами сравнивать два вектора. Методы AddVector, SubtractVector, CrossProduct, и DotProduct реализуют основные векторные операции — сложение и вычитание, векторное и скалярное произведения векторов. Объект Vector (в отличие от единичного вектора UnitVector) поддерживает ряд методов и свойств, связанных с его длиной. Это Length, Normalize (приведение вектора к единичной длине или нормализация) и ScaleBy (умножение вектора на скаляр). Наконец, поддерживаются операции преобразования типа векторов. Из объекта Vector с помощью метода AsUnitVector можно получить объект UnitVector, тогда как метод AsVector наоборот приводит тип UnitVector к типу Vector.
Матрицы (Matrix)
[править]Матрицы очень широко применяются в задачах точного позиционирования и изменения ориентация компонентов в сборках Инвентора.
Матрица представляет собой двумерный массив чисел. Для трехмерного пространства Инвентор поддерживает объект Matrix, для двумерных пространств предусмотрен объект Matrix2d. Объект Matrix представляет собой матрицу размерностью 4x4 (4 строки и 4 столбца). Объект Matrix2d представляет собой матрицу размерностью 3x3. Ниже показана типичная 3D-матрица 4x4.
Объект Matrix инкапсулирует в себе 16 значений и выглядит довольно просто. Тем не менее, из всей вспомогательной геометрии именно матрицы оказываются наименее очевидными объектами, освоение которых обычно требует некоторых усилий.
В зависимости от решаемой задачи можно рассматривать матрицы с двух точек зрения. В первом случае матрица служит инструментом для задания системы координат. Во втором случае матрица описывает некоторое геометрическое преобразование.
Первый подход является самым простым и наиболее полезным. Рассмотрим, из чего состоит система координат, и каким образом матрица обеспечивает требуемую информацию. Координатная система описывает положение и ориентацию в пространстве. В трехмерном пространстве начало координат есть трехмерная координатная точка , заданная в пространстве модели. Она задает положение системы координат. Ориентация системы координат описывается направлениями главных осей , и .
В ортогональных системах координат, которые всегда используются Инвентором, действует ряд упомянутых выше жёстких правил, а именно, оси , и являются взаимно перпендикулярными, а направление оси удовлетворяет правилу правой руки. Все три вектора направлений являются единичными.
Следующий рисунок показывает, каким образом матрица хранит геометрическую информацию о системе координат. Во-первых, при использовании матрицы вы можете игнорировать нижнюю строку. В ней всегда хранятся одни и те же значения 0, 0, 0, 1. Остальные 12 значений определяют координатную систему. Первый столбец описывает компоненты направления оси (1,0,0). Второй столбец задает направление оси (0,1,0), третий — оси (0,0,1). Последний столбец определяет положение начала системы координат (0,0,0). Показанная справа матрица называется единичной. Начало координат и направления единичных векторов совпадают с базовой системой координат. Такая матрица не описывает ни перемещения, ни вращения.
Как будет выглядеть матрица для задания системы координат с началом в точке (10,5,0) и повёрнутой на 45° вокруг оси ?
Рассмотрим сначала ось . Если новая система координат повернута на 45° вокруг оси , значит и ось повернута относительно базовой оси на 45° в положительном направлении отсчета углов. Таким образом, ось направлена в направлении вектора (1, 1, 0), но поскольку вектор системы координат должен быть единичным, то результат должен выглядеть так (0.707, 0.707, 0). Соответственно, ось имеет отрицательную компоненту по и положительную по и будет выглядеть следующим образом (-0.707, 0.707, 0). Ось направления не меняет (0, 0, 1). Наконец, в четвертом столбце вписываются координаты точки начала системы координат (10, 5, 0).
Приведенный ниже фрагмент кода демонстрирует технику применения средств API для формирования описанной матрицы. Во-первых, для задания осевых векторов применяются объекты UnitVector. Это гарантирует, что все векторы, как и требуется, будут единичными. Во-вторых, для задания матрицы используется метод SetCoordinateSystem объекта Matrix, что упрощает заполнение матрицы значениями.
При задании координатной системы не следует забывать, что все геометрические величины задаются во внутренних единицах Инвентора, в частности, длины всегда задаются в сантиметрах.
Public Sub MatrixDefineSample()
' ссылка на вспомогательную геометрию и создание переменной для числа Pi
Dim oTG As TransientGeometry
Set oTG = ThisApplication.TransientGeometry
Dim dPi As Double
dPi = Atn(1) * 4
' Точка начала координат
Dim oOrigin As Point
Set oOrigin = oTG.CreatePoint(10, 5, 0)
' Задание осевых векторов
Dim oXAxis As UnitVector
Dim oYAxis As UnitVector
Dim oZAxis As UnitVector
Set oXAxis = oTG.CreateUnitVector(Cos(dPi / 4), Sin(dPi / 4), 0)
Set oYAxis = oTG.CreateUnitVector(-Cos(dPi / 4), Sin(dPi / 4), 0)
Set oZAxis = oTG.CreateUnitVector(0, 0, 1)
' Создание матрицы с описанием новой системы координат
Dim oMatrix As Matrix
Set oMatrix = oTG.CreateMatrix
Call oMatrix.SetCoordinateSystem( _
oOrigin, oXAxis.AsVector, oYAxis.AsVector, oZAxis.AsVector)
End Sub
Вместо использования метода SetCoordinateSystem вы вольны сформировать матрицу поэлементно. Доступ к ячейкам матрицы на чтение и запись обеспечивает свойство Matrix.Cell. Приведенный ниже фрагмент кода поэлементно формирует ту же самую матрицу, что и предыдущая программа с помощью метода SetCoordinateSystem. Легко видеть, что вариант с SetCoordinateSystem проще и «читабельней». Тем не менее, применение Matrix.Cell может оказаться вполне уместным в случае внесения в ячейки матрицы малых изменений.
' Создание матрицы с описанием новой системы координат Dim oMatrix As Matrix Set oMatrix = oTG.CreateMatrix oMatrix.Cell(1, 1) = oXAxis.X oMatrix.Cell(2, 1) = oXAxis.Y oMatrix.Cell(3, 1) = oXAxis.Z oMatrix.Cell(1, 2) = oYAxis.X oMatrix.Cell(2, 2) = oYAxis.Y oMatrix.Cell(3, 2) = oYAxis.Z oMatrix.Cell(1, 3) = oZAxis.X oMatrix.Cell(2, 3) = oZAxis.Y oMatrix.Cell(3, 3) = oZAxis.Z oMatrix.Cell(1, 4) = oOrigin.X oMatrix.Cell(2, 4) = oOrigin.Y oMatrix.Cell(3, 4) = oOrigin.Z
Приведенная ниже отладочная процедура DumpMatrix также весьма полезна при работе с матрицами. Она выводит в отформатированном виде содержимое матрицы.
Public Sub DumpMatrix(oMatrix As Matrix)
Dim i As Integer
For i = 1 To 4
Debug.Print Format(oMatrix.Cell(i, 1), "0.000000") & ", " & _
Format(oMatrix.Cell(i, 2), "0.000000") & ", " & _
Format(oMatrix.Cell(i, 3), "0.000000") & ", " & _
Format(oMatrix.Cell(i, 4), "0.000000")
Next
End Sub
Для матрицы в нашем примере DumpMatrix выведет следующие результаты
0.707107, -0.707107, 0.000000, 10.000000 0.707107, 0.707107, 0.000000, 5.000000 0.000000, 0.000000, 1.000000, 0.000000 0.000000, 0.000000, 0.000000, 1.000000
Чаще всего матрицы применяются при работе с компонентами сборок, а именно, матрицы используются для задания положения и ориентации вставляемых в сборку компонентов. Рассмотрим конкретный пример, используя деталь, показанную на следующем рисунке. Детали подобной формы оказываются полезными при отладке использующих матрицы программ, поскольку прекрасно визуализируют ориентацию системы координат и результаты манипуляций с матрицами. Деталь сконструирована так, что начало координат находится на пересечении стрелок, а длинная стрелка направлена вдоль оси .
Если вы откроете новую сборку и вручную вставите в сборку экземпляр такой детали, то увидите, что компонент оказался в начале координат сборки, а ориентация системы координат компонента будет эквивалентна ориентации системы координат сборки. Дело в том, что для позиционирования первого компонента Инвентор использует единичную матрицу. Если мы добавим к предыдущей программе следующий фрагмент кода, деталь будет вставлена в точке (10,5,0) и повернута вокруг оси на 45°.
' вставка компонента в активную сборку с помощью заданной матрицы
Dim oOcc As ComponentOccurrence
Set oOcc = ThisApplication.ActiveDocument.ComponentDefinition. _
Occurrences.Add("C:\Temp\Arrow.ipt", oMatrix)
В результате будет получена сборка, в которой компонент справа вверху был вставлен средствами API.
Изменяя матрицу компонента, можно переопределять его положение в сборке. Свойство Transformation объекта ComponentOccurrence обеспечивает доступ к матрице на чтение и запись. Ниже приведены несколько примеров изменения положения компонента.
Public Sub ModifyOccurrence()
' Ссылка на активную сборку
Dim oAsmDoc As AssemblyDocument
Set oAsmDoc = ThisApplication.ActiveDocument
' Ссылка на существующий компонент "Arrow:1"
Dim oOcc As ComponentOccurrence
Set oOcc = oAsmDoc.ComponentDefinition.Occurrences.ItemByName("Arrow:1")
Dim oTG As TransientGeometry
Set oTG = ThisApplication.TransientGeometry
' перемещение в точку (3,2,1).
Dim oMatrix As Matrix
Set oMatrix = oOcc.Transformation
Call oMatrix.SetTranslation(oTG.CreateVector(3, 2, 1))
oOcc.Transformation = oMatrix
' Смещение компонента на 5 см вдоль оси X
' непосредственным редактированием его матрицы
Set oMatrix = oOcc.Transformation
oMatrix.Cell(1, 4) = oMatrix.Cell(1, 4) + 5
oOcc.Transformation = oMatrix
End Sub
Матрица преобразования
[править]Другой вариант интерпретации матриц — матрица задает изменение положения и ориентации. Этот подход концептуально иной, нежели использование матриц для задания систем координат, поскольку задается не абсолютное положение, а изменение положения. Чтобы это сделать, вы создаете матрицу, которая определяет желаемое изменение, а затем применяете его к другой матрице.
Приведем пример для демонстрации этого подхода. Положим, вы желаете переместить некоторые детали в сборке на 5 см вдоль оси . Одно решение базируется на информации, которую мы узнали ранее о матрицах для задания системы координат. Оно заключается в непосредственном редактировании матрицы, чтобы переместить систему координат компонента не 5 см вдоль положительного направления оси .
' Последовательный перебор компонентов сборки Dim oOcc As ComponentOccurrence For Each oOcc In oAsmDoc.ComponentDefinition.Occurrences ' Получение матрицы текущего компонента Dim oMatrix As Matrix Set oMatrix = oOcc.Transformation ' Изменение ячейки матрицы, которая отвечает за положение ' начала системы координат компонента относительно оси X oMatrix.Cell(1, 4) = oMatrix.Cell(1, 4) + 5 ' Переопределение свойства Transformation ' компонента с помощью изменённой матрицы. oOcc.Transformation = oMatrix Next
Второе решение той же задачи основано на преобразовании текущей ориентационной матрицы компонента.
' Создание матрицы, которая описывает преобразование.
Dim oTransMatrix As Matrix
Set oTransMatrix = ThisApplication.TransientGeometry. _
CreateMatrix oTransMatrix.Cell(1, 4) = 5
' Последовательный перебор компонентов сборки
Dim oOcc As ComponentOccurrence
For Each oOcc In oAsmDoc.ComponentDefinition.Occurrences
' получение матрицы текущего компонента
Dim oMatrix As Matrix
Set oMatrix = oOcc.Transformation
' Применение матрицы преобразования oTransMatrix
Call oMatrix.TransformBy(oTransMatrix)
' Переопределение свойства Transformation
' компонента с помощью изменённой матрицы.
oOcc.Transformation = oMatrix
Next
Обе программы дают одинаковые результаты. Для столь простой задачи первое решение выглядит несколько проще. Однако, если требуемое преобразование окажется заметно сложнее, чем тривиальное перемещение, то использование матрицы преобразования становится уже заметно легче, чем перевычисление каждый раз системы координат. Ниже будет показано, как для сложных преобразований можно в одной матрице комбинировать несколько преобразований.
Продемонстрируем «упаковку» последовательных преобразований в одной матрице. Предположим, нам необходимо повернуть компонент на 45° вокруг оси , затем на 30° вокруг оси , после чего переместить его на 5 см вдоль оси и на 3 см вдоль оси . Как мы могли бы определить матрицу, выполняющую такое преобразование? Гораздо проще определить каждое из последовательных преобразований отдельно, а затем применить функционал матриц, чтобы вычислить итоговую матрицу комбинированного преобразования. Умножение матриц порождает новую матрицу, которая содержит преобразование-комбинацию исходных. Порядок матриц-сомножителей имеет значение, поскольку влияет на результат. Данная операция выполняется с помощью метода TransformBy. Метод выполняет умножение матрицы-аргумента на текущую. В общем случае, вы имеете матрицу и преобразуете ее, изменяя с помощью другой матрицы. Рассмотрим, как это работает на практике при решении поставленной выше задачи.
Dim dPi As Double
dPi = Atn(1) * 4 'Число Пи
'ссылка на вспомогательную геометрию
Dim oTG As TransientGeometry
Set oTG = ThisApplication.TransientGeometry
' Создание матрицы для поворота на 45° вокруг оси x
Dim oTransMatrix As Matrix
Set oTransMatrix = oTG.CreateMatrix
Call oTransMatrix.SetToRotation(dPi / 4, _
oTG.CreateVector(1, 0, 0), _
oTG.CreatePoint(0, 0, 0))
' Создание матрицы для поворота на 30° вокруг оси y.
Dim oTempMatrix As Matrix
Set oTempMatrix = oTG.CreateMatrix
Call oTempMatrix.SetToRotation(dPi / 6, _
oTG.CreateVector(0, 1, 0), _
oTG.CreatePoint(0, 0, 0))
' Изменение матрицы oTransMatrix матрицей oTempMatrix
Call oTransMatrix.TransformBy(oTempMatrix)
' Создание матрицы перемещения на 5 см по x и 3 см по z.
oTempMatrix.SetToIdentity
Call oTempMatrix.SetTranslation(oTG.CreateVector(5, 0, 3))
' Применение трансляционного преобразования
Call oTransMatrix.TransformBy(oTempMatrix)
' Цикл по компонентам сборки
Dim oOcc As ComponentOccurrence
For Each oOcc In oAsmDoc.ComponentDefinition.Occurrences
' Получение копии ориентационной матрицы очередного компонента
Dim oMatrix As Matrix
Set oMatrix = oOcc.Transformation
' модифицирование матрицы-копии
Call oMatrix.TransformBy(oTransMatrix)
' Переопределение ориентационной матрицы компонента измененной копией.
oOcc.Transformation = oMatrix
Next
Этот пример не слишком отличается от предыдущего, за исключением процедуры формирования матрицы комбинированного преобразования последовательностью матричных операций. Чтобы облегчить нашу задачу, использованы и некоторые другие функции объекта Matrix. Например, для описания вращения применён метод SetToRotation, а для превращения матрицы в единичную — метод SetToIdentity. Матрицы, определяющие геометрические преобразования, часто используются в Инвенторе и для задания преобразования из одной системы координат в другую. Это позволяет несколько иначе взглянуть на позиционирование компонента в процессе его вставки в сборку с использованием матрицы. Геометрия детали определена в системе координат этой детали. Матрица, которая определяет положение детали в сборке, описывает преобразование из системы координат детали в систему координат сборки. Вот простая иллюстрация на эту тему.
Public Sub ModelPointInAssembly() Dim oAsmDoc As AssemblyDocument Set oAsmDoc = ThisApplication.ActiveDocument ' Получим ссылку на компонент сборки. ' Здесь мы просто выберем первый по списку. ' Чтобы результат был интереснее, компонент будет ' смещён и повёрнут относительно исходного положения. Dim oOcc As ComponentOccurrence Set oOcc = oAsmDoc.ComponentDefinition.Occurrences.Item(1) ' Создадим координатную точку с координатами (0,0,0) ' Она будет представлять начало системы координат детали. Dim oPartOrigin As Point Set oPartOrigin = ThisApplication.TransientGeometry.CreatePoint(0, 0, 0) ' Получим матрицу компонента. Она описывает его ' положение в системе координат сборки. ' Эта матрица определяет и преобразование из системы ' координат детали в систему координат сборки Dim oTransMatrix As Matrix Set oTransMatrix = oOcc.Transformation ' Применим преобразование к точке oPartOrigin. ' Это преобразует её к системе координат сборки. Call oPartOrigin.TransformBy(oTransMatrix) ' Создадим видимую фиксированную рабочую точку ' чтобы увидеть новое положение начала координат детали Call oAsmDoc.ComponentDefinition.WorkPoints.AddFixed(oPartOrigin) End Sub
Матрица, возвращаемая свойством ComponentOccurrence.Transformation, описывает преобразование из системы координат детали в систему координат сборки. Возможна и обратная операция, если вы имеете точку в пространстве сборки и хотите узнать ее координаты в пространстве детали. Объект Matrix поддерживает метод Invert. Метод преобразует матрицу для выполнения обратного преобразования. Обращение (инвертирование) матрицы, возвращаемой объектом ComponentOccurrence, определяет преобразование из пространства сборки в систему координат детали.
Inventor API поддерживает матрицы, которые определяют преобразования
- из пространства детали в пространство сборки,
- из пространства модели (детали или сборки) в пространство вида чертежа,
- из пространства модели в пространство листа,
- из пространства вида в пространство модели,
- из пространства листа в пространство модели,
- из пространства вида в пространство листа,
- из пространства листа в пространство вида,
- из пространства эскиза в пространство модели,
- из пространства модели в пространство эскиза.
Матрицы применяются также для получения данных о положении элементов массивов, для задания положения клиентской графики, эскизных обозначений, текстурных карт и титульных надписей.
Литература
[править][1] Brian Ekins. How Deep is the Rabbit Hole? Examing the Matrix and other Inventor® Math and Geometry Objects. Лекция DE205-2, Autodesk University 2008.