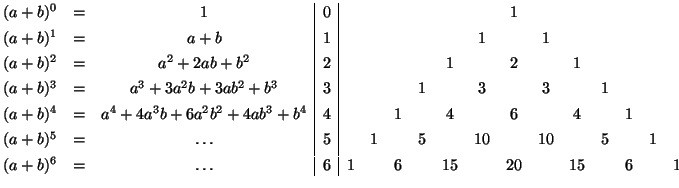Язык Си в примерах/Треугольник Паскаля

Материал из Викиучебника

Всем известны простые формулы

• (a + b)² = a² + 2ab + b²
• (a + b)³ = a³ + 3a²b + 3ab² + b³

А как находить коэффициенты в разложении (a + b)ⁿ?

Рассмотрим следующую таблицу:

То, что нарисовано справа, называется треугольником Паскаля — в n-й строчке этого треугольника находятся коэффициенты для разложения .

Число номер k + 1 в n-й строчке называется биномиальным коэффициентом .

Например,

Стороны треугольника Паскаля состоят из единичек. Каждое число внутри треугольника Паскаля равно сумме двух чисел, стоящих над ним справа и слева в предыдущей строчке:

Эти числа возникают в задаче о числе сочетаний: — это число способов выбрать k элементов из n различных. Например, чиcло байт, в которых ровно 3 единицы — это число — число способов выбрать три бита, в которых будут стоять единицы, из воcьми бит байта.

Докажите, что

Рассмотрим две программы, которые решают следующие задачи:

1. Запрограммировать функцию .
2. Вывести на экран n строчек треугольника Паскаля.

 /*
   Вычисление биномиальных коэффициентов.
 */
 #include <stdio.h>
 long C(long n,long k) {
    if(k == 0 || n == k) return 1;
    return C(n - 1, k - 1) + C(n - 1, k);
 }
 int main() {
    long n, k;
    scanf ("%ld%ld", &n, &k);
    printf ("%ld ", C(n, k));
    return 0;
 }

• Сколько раз вызовется функция C(., .) при вычислении С(n, k)?
• Докажите, что время вычисления по приведенному алгоритму пропорционально .
• Оцените ассимптотику , а именно, напишите программу, которая вычисляет для n = 2,4,...,40 и нарисуте график

от n.

 /*
     Вычисление <i>n</i>-й строки треугольника Паскаля.
 */
 #include <stdio.h>
 #define N 1000
 long c[N];
 int main () {
    long n, i, j;
    scanf ("%ld",&n);
    for(i = 1; i <= n ; i++) c[i] =0;
    c[0] = 1;
    for(j = 1 ; j <= n; j++)
       for(i = j; i >= 1 ; i--)
          c[i] = c[i-1] + c[i];
    for(i = 0; i <= n ; i++)
       printf ("%ld ", c[i]);
    return 0;
 }

• Докажите, что указанный алгоритм вычисления n-й строчки треугольника Паскаля

работает быстрее, чем алгоритм вычисления из предыдущей программы, а именно время работы пропорционально .

• Начиная с какого n самое большое число из n-й строчки треугольника Паскаля не умещается в тип long?