Трудные темы курса физики/Траектория
Траектория представляет собой понятие, непосредственно связанное с перемещением (позднелат.-trajektorius т.е.имеющий отношение к движению) Поэтому траектория есть непрерывная линия, по которой движется геометрическая точка в пространстве.([1] Стр.764 ).Существенно, что положение геометрической точки в данный момент времени не может быть описано иначе, как по отношению к заданной системе координат в трёхмерном пространстве, а её перемещение - как изменение этих координат во времени.
Траектория является объектом изучения раздела механики -кинематики, посвящённой изучению геометрии движения тел без учёта их масс и причин, вызывающих это движение, т.е. без учёта действующих на эти тела сил.[1] Стр.281 )
Траектория в кинематике движения тел
[править]Наиболее употребительными являются декартовы прямоугольные системы координат и сферические системы координат.
Декартовы системы координат образованы тремя взаимно пересекающимися в одной точке , называемой началом координат координатными осями. В зависимости от взаимного расположения выбранных за положительное направление, различают правую и левую систему декартовых координат. По умолчанию принята правая система координат, ассоциируемая с правой резьбой или правилом буравчика. А именно положительным направлением оси Z считается такое, по которому движется буравчик, если он совершает поворот от оси X по направлению к оси Y.Это направление вращения считается положительным.В таком случае положение точки задаётся тремя числами, соответствующим проекциям точки (или конца радиуса-вектора) на соответствующие оси.
Иногда положение точки в этой системе координат задают радиусом-вектором, имеющим началом (полюсом) начало системы координат, а конец - в данной точке.
Сферическая полярная система координатТакже имеет своей основой декартову систему, но в качестве координат выступают: длина радиуса-вектора , долгота и полярное расстояние . При этом долгота измеряется углом поворота проекции радиуса-вектора на плоскость XOY в положительном направлении, а полярное расстояние - угол поворота самого радиуса-вектора от оси OZ.
Чрезвычайно распространено изображение проекции точки на плоскость чертежа, за которую общепринято брать плоскость XOY, что значительно повышает наглядность решаемой задачи в этом случае имеют дело с декартовыми системами координат на плоскости и полярными системами координат.[2]
- При этом следует учитывать и всегда помнить , что такое упрощение в ряде задач сопровождается полной потерей информации о явлениях, принципиально происходящих в трёхмерном пространстве, в том числе описание которых зависит от выбора правой или левой системы координат.
Движение геометрической точки можно представить, как изменение её координат во времени. Так, например, векторное уравнение представляет собой закон движения геометрической точки в его векторном описании.Исключив из этого уравнения время можно получить годограф точки или её траекторию.([1] Стр. 282)
- Траектория геометрической точки описывается математическим выражением закона её движения, из которого исключено время.Итак, траекто́рия материа́льной то́чки — есть кривая линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта.Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения.Так улица, в начале которой висит знак «кирпич» останется в принципе траекторией движения по ней.
Выше рассматривалась свободная геометрическая точка, координаты которой могли свободно изменяться во времени. В таком случае принято говорить,что она располагала тремя степенями свободы.
Однако весьма часто на возможные её координаты налагаются ограничения, предопределяющие форму её траектории. В этом случае положение точки определяется её расстоянием от некоторого начального положения на её траектории.В этом случае имеют дело с естественным или траекторным описанием движения, что может быть представлено графиком на плоскости , где в прямоугольной системе координат по оси абсцисс отложено время, а по оси ординат - расстояние, проходимое точкой в направлении, принятом за положительное, и в этом случае являющееся единственной координатой, описывающей положение точки.([1]Стр. 282)
Наиболее популярным физическим объектом является материальная точка, т.е. геометрическая (и потому не имеющая размеров), но наделённая массой.Она имеет тоже лишь три степени свободы.
В случае, когда геометрическими размерами материального тела пренебречь по условиям задачи нельзя, его рассматривают как совокупность материальных точек.Что имеет смысл, например, в небесной механике по отношению к Солнечной системе.Говорить о траектории такого материального тела в межзвёздном пространстве без существенных упрощений крайне трудно .
Полезным приёмом является и модель абсолютно твёрдого тела, в котором взаимное расположение его частей остаётся неизменным даже в случае внешнего на него воздействия (т.е. недеформируемости тела).В таком случае рассматривается движение некоторой его характерной точки, что позволяет говорить о траектории тела. Во многих случаях за такую точку принимается центр масс тела. Если на движение такого материального тела не наложено никаких ограничений, то оно имеет шесть степеней свободы. А именно -три степени свободы его центра масс и три эйлеровых угла. Их находят, совместив с телом координатную систему XYZ, которая в новом положении обозначается , как X’ Y’ Z’ А именно: Угол нутации (выше полярное расстояние , угол прецессии определяемый как угол между осью OX и следом пересечения OA плоскостей XOYи X’ O Y’так, что прямые OA, OZ, OZ’ образуют тройку правой ориентации и, наконец, угол чистого вращения (правильнее было бы говорить угол чистого поворота, но это не принято ) .В соответствие с теоремой вращения Эйлера любой поворот тела имеет ось вращения OZ’. [2]
- Значительно реже в качестве такого элементарного физического тела рассматривается 'галтель,представляющая собой тело , имеющее длину, но высоту и ширину настолько малые, что этими размерами можно пренебречь. В качестве таких тел рассматриваются, например, диполи, представляющие собой поляризованные молекулы. Такие тела считаются не имеющими чистого вращения и потому обладающими пятью степенями свободы.
Специфическим видом движения тела является так называемое Поступательное движение — механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени, при котором любая прямая, соединяющая любые две точки пространства перемещается параллельно самой себе.Нередко такой вид движения противопоставляется движению со вращением,([1] страница 282.)
Существенно, что поступательное движение есть единственная разновидность движения трёхмерного тела, когда можно говорить о его траектории, поскольку все его точки движутся по одинаковым (при наложении совпадающим ) траекториям. Более того, только при таком движении тела можно говорить о его скорости и ускорении.Во всех остальных случаях эти понятия для пространственного тела теряют смысл. [3]
И это можно было бы принять, поскольку по определению вращение есть такое движение тела, при котором остаётся неподвижной по крайней мере одна точка тела.При поступательном движении таких точек нет, и все точки тела меняют своё положение в пространстве.Однако вращение вокруг собственной оси и одновременное вращение с той же угловой скоростью в обратном направлении вокруг точки вне тела может дать перенос, то есть поступательное движение. Что имеет мест в случае с велосипедной педалью. Поэтому заявлять, что поступательное движение исключает вращение и является ему альтернативой неверно.
С другой стороны, движение тела в пространстве, изображённое на Рис.2, можно повторить и без сложения нескольких поворотов, а просто взяв тело рукой и совершив ею соответствующее сложное движение.Или соответствующим образом запрограммировать робот, задав координаты его исполнительного органа параметрически как функцию времени, не используя представление о движении по дуге окружности даже в математической записи формулы траектории.
Траектория материальной точки в общем случае представляющая собой пространственную кривую, которую можно представить в виде сопряжённых дуг различного радиуса, исходящего каждый из своего центра, положение которого может меняться во времени. В пределе и прямая может рассматриваться как дуга, радиус которой равен бесконечности
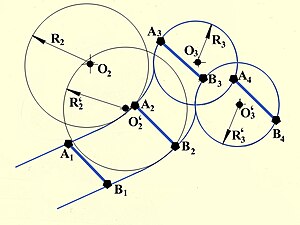
Приведённая иллюстрация показывает, что, в отличие от распространённого утверждения поступательное движение не является противоположностью движению вращательному. Что многократно растиражировано литературой по физике, в том числе в массовых учебниках, и представляет собой наглядный пример того, как осторожно надо подходить к выяснению смысла используемых в них фундаментальных понятий.
При этом подразумевается, что прямолинейное движение есть поворот вокруг бесконечно удалённого от тела центр поворота|центра поворота.Оказывается, что при поступательном движении в каждый заданный момент времени любая точка тела совершает поворот вокруг своего мгновенного центра поворота, причём длина радиуса в данный момент одинакова для всех точек тела. Одинаковы по величине и направлению и векторы скорости точек тела, а также испытываемые ими ускорения.

В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе,(что находит своё выражение в сохранении постоянства Эйлеровых углов) остаётся в силе.
В общем виде траектория тела представляет собой гладкую пространственную кривую, свойства которой в каждой точке (за исключением особых точек) на основании положений дифференциальной геометрии кривых описываются сопровождающим трёхгранником , образованным взаимно перпендикулярными единичными векторами. А именно вектором касательной , вектором главной нормали и вектором бинормали , перпендикулярным так называемой соприкасающейся плоскости, в которой лежат векторы касательной и нормали. Таким образом при своём перемещении по кривой сопровождающий трёхгранник осуществляет поворот вокруг бинормали и кручение в нормальной плоскости, проходящей через нормаль и бинормаль.[2]
И поворот и кручение оцениваются в угловой мере и их производные во времени определяют угловые скорости сложного вращения, результирующая угловая скорость которого представляет собой векторную их сумму.
Если тело движется поступательно, то для описания его движения достаточно описать движение произвольной его точки (например, движение центра масс тела)и вращательного движения самого тела вокруг центра масс (это обстоятельство принято во внимание при формулировке теоремы Кёнига.
Математически поступательное движение по своему конечному результату эквивалентно параллельному переносу. Однако, рассматриваемое как физический процесс оно представляет собой в трёхмерном пространстве вариант винтового движения (См. Рис. 2)
Моделью поступательного движения в первом приближении (если пренебречь качанием ступни) является педаль велосипеда, совершающая при этом за полный цикл своего хода один поворот вокруг своей оси.
Траектория в различных системах координат
[править]
Кроме того, и при наличии движущегося по ней объекта, траектория, изображаемая в наперёд заданной системе пространственных координат, сама по себе не может ничего определённого сказать в отношении причин его движения, пока не проведён анализ конфигурации поля действующих на него сил в той же координатной системе.
Так поезда разной массы, движущиеся под различными тяговыми усилиями на сцепных крюках локомотивов и потому с разной скоростью, будут двигаться по одной и той же траектории, определяемой формой рельсового пути, налагающего на движение несвободного тела (поезда) конкретные связи, интенсивность которых будет в каждом случае различной.
Не менее существенно, что форма траектории неотрывно связана и зависит от конкретной системы отсчёта, в которой описывается движение.Так, Луна обращается вокруг Земли только в системе отсчёта, связанной с их общим центром гравитации (находится внутри Земного шара). В системе же отсчёта, началом которой является Солнце, Луна обращается вокруг него по той же эллиптической орбите, что и Земля, но с периодическими отклонениями от неё на величину расстояния от Луны до Земли.К тому же движется он неравномерно, обгоняя Землю с максимальной скоростью в полнолуние и начиная отставать в новолуние.
Никакого взаимного обращения этих небесных тел в этом случае просто нет.Наличие земного притяжения для объяснения формы траектории Луны в системе координат, связанной с Солнцем, вообще не обязательно. Так, исчезни Земля, Луна могла бы продолжать двигаться, как самостоятельное небесное тело, по той же самой старой траектории, а её периодические возмущения можно было бы тогда в качестве гипотезы объяснить изменением силы тяготения, скажем, за счёт вариации массы Солнца по причине пульсации его светимости (что, кстати, и наблюдается в определённых пределах в действительности).
И обе упомянутые формы траектории истинны и оба объяснения их формы на основании правильно проведённого анализа действующих сил справедливы. Но они исключают друг друга, как исключается возможность одновременного рассмотрения при выборе той или иной системы координат.
Возможно наблюдение траектории при неподвижности объекта, но при движении системы отсчёта. Так, при длительной экспозиции эти звёзды представляются движущимися по круговым траекториям. Не каждый решится объяснить это действием центростремительной силы с центром в Полюсе Мира в районе Полярной звезды.
Возможен и случай, когда тело явно движется, но траектория в проекции на плоскость наблюдения является одной неподвижной точкой. Это, например, случай летящей прямо в глаз наблюдателя пули или уходящего от него поезда.
Траектория в динамике движения тел
[править]До Ньютона причиной движения любого материального тела была постоянно действующая на него сила. Если сила исчезала, по общему мнению тело должно было остановиться. Ньютон радикально изменил взгляд на движение тел, заявив, что сила есть причина изменения движения тела. При этом в качестве системы отсчёта он рассматривал в соответствие с воззрениями своего времени заполняющий всё пространство Вселенной эфир. А связанная с ним система отсчёта есть Абсолютная система отсчёта (АИСО), которую можно считать исходной для рассмотрения любого движения.
В соответствие с установленным им Первым законом (называемым ещё законом инерции), любое материальное тело , находящееся в такой системе отсчёта, сохраняет состояние покоя или равномерного прямолинейного движения пока и поскольку действующей на него силой не будет выведено из этого состояния.
Ещё Галилей обратил внимание на то, что пассажир, находящийся внутри замкнутого помещения на корабле не может, наблюдая за падением тел, сказать, неподвижен ли корабль или же движется относительно другого, в том числе и стоящего на якоре.На этом мысленном эксперименте (нем. Gedankenexperiment в формулировке Маха) основан так называемый Принцип относительности Галилея в классической механике, согласно которому законы механики не зависят от того, в какой из инерциальных систем отсчёта они наблюдаются.
Из этого следует, что свойством быть инерциальной обладает бесконечное множество систем отсчёта, движущихся по отношению к Абсолютной равномерно и прямолинейно.И каждую из них можно назвать инерциальной (ИСО). Замечательной особенностью инерциальных систем отсчёта является то обстоятельство, что траектория тела, имеющая вид прямой линии, сохраняет свою прямолинейность в любой другой инерциальной системе. Может меняться её направление, скорость и длина пройденного телом пути, но прямолинейность сохранится.
В дальнейшем экспериментально было доказано (эксперимент Майкельсона-Морли), что скорость света в любой системе отсчёта остаётся неизменной и потому эфир не существует. Не существует и АИСО и потому все инерциальные системы равноправны.
По традиции принято по умолчанию рассматривать движение тела в ИСО. Тогда, если тело движется с непостоянной скоростью, как вектором , в том числе меняет направление, т.е. движется по криволинейной траектории, причиной этого считается не уравновешенное взаимное действие на него сил.
Обратное утверждение справедливо не всегда. Тело может находиться в состоянии относительного равновесия, т.е. быть неподвижным в избранной системе координат, которая не инерциальна (неинерциальная система координат - НСО). Примером тому является любой неподвижный материальный объект, принимающий участие во вращении Земного шара. Его неподвижность определяется балансом действующих на него сил: центростремительной, созданной силой гравитации и силой реакцией опоры - с одной стороны и центробежной силой инерции-с другой.([4] стр.159)
Второй закон Ньютона представляет собой выражение концепции Ньютона, ставшей основой классической механики, заключающейся в пропорциональности ускорения, приобретаемого телом, действующей на него результирующей силе.При этом происхождение силы никак не специфицируется и это делает его всеобщим, применимым к движению тел в любой системе отсчёта, как в ИСО, так и НСО ([4] стр.132 -134)
Ключевым моментом в решении вопроса о форме траектории при переходе от одной системы отсчёта к другой является то обстоятельство, что принцип Галилея соблюдается для каждой из них, но совсем не должен выполняться при переходе из одной в другую.Так, например, для пассажира в движущемся равномерно и прямолинейно автомобиле колесо обладает некоторым запасом кинетической энергии вращения. Но для неподвижно стоящего наблюдателя к этой кинетической энергии добавляется ещё и кинетическая энергия , пропорциональная квадрату скорости движения колеса как составной детали автомобиля,
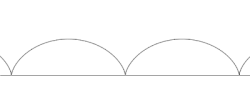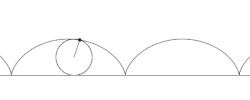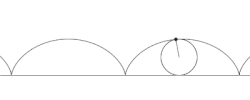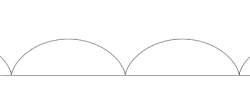
Для неподвижного наблюдателя движение любой точки на периферии колеса, описывается циклоидой.Но связать её с качением колеса движущегося без проскальзывания,он может только на основании собственного участия в наблюдении движущегося автомобиля. Если же ему траектория будет представлена в виде графика, то он с тем же основанием может сказать, что она никакого отношения к явлению качения не имеет. Но есть просто нарисованная волнистая линия. Более того, попытавшись объяснить её происхождение, он сопоставит её появление с движением карандаша под действием переменной во времени силы, которая определенно становится равной нулю, когда карандаш в точке перегиба меняет направление своего движения.Хотя для движущегося с автомобилем наблюдателя ясно, что движение интересующей каждого из них точки вызвано неизменной во времени центростремительной силы. И это при том, что оба наблюдателя находятся в совершенно равноправных инерциальных системах.
- Таким образом достаточно полное представление о действующих на тело силах позволяет путём решения уравнений движения построить траекторию движения тела. Но создать однозначное мнение о действовавших на тело в процессе его движения силах на основе его траектории и без получения дополнительной информации не представляется возможным.
Литература
[править]- ↑ а б в г д Физический энциклопедический словарь/ Гл. ред. А.М.Прохоров. Ред.кол. Д.М.Алексеев, А.М. Бонч-Бруевич,А.С.Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил.
- ↑ а б в Бронштейн И.Н. Семендяев К.А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
- ↑ Тарг Семён Михайлович. Краткий курс теоретической механики М., Л.: Государственное издательство физико-математической литературыю 1961.
- ↑ а б Хайкин, Семён Эммануилович|С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы.









