Трудные темы курса классической механики/Кинематика

Кинематика представляет собой раздел механики, предметом которого является описание движения тел, но не причин такого движения.

В полном соответствии с дифференциальным подходом в описании явлений, в механике вводится понятие о материальной точке, как объекте, размерами которого можно пренебречь, но который обладает конечной величиной массы покоя.

Движение тела можно количественно описать в том случае, если задан способ устанавливать его положение в пространстве по отношению к другим телам, называемым телами отсчёта.С материальными точками, представляющими такие тела принято сопоставлять геометрическую конструкцию,называемую Системой отсчёта. В кинематике все принятые системы отсчёта, позволяющие однозначно локализовать положение материальной точки в заданный момент времени равноправны. Однако в динамике постоянно приходится иметь дело с наличием определённой разницы при выборе адекватной решаемой задаче системы отсчёта. Это различие заключено в определении допустимой степени инерциальности используемой неинерциальной системы , которая лишь с некоторой степенью точности может считаться системой инерциальной.

В случае, когда геометрическими размерами материального тела пренебречь по условиям задачи нельзя, его рассматривают как совокупность материальных точек.Что имеет смысл, например, в небесной механике по отношению к Солнечной системе, где в ряде случаев не только планеты, но и само Солнце рассматриваются как материальные точки.

Полезным приёмом является и модель абсолютно твёрдого тела, в котором взаимное расположение его частей остаётся неизменным даже в случае внешнего на него воздействия (т.е. не деформируемости тела).

Нередко можно натолкнуться на утверждение, что использование представления об абсолютной твёрдости рассматриваемого в своём движении тела позволяет, выделив в нём характерную точку, например центр масс тела, говорить о траектории движения тела. Такое заявление справедливо лишь в исключительном случае поступательного движения. В общем случае,то есть когда тело совершает поворот, его отдельные точки движутся по разным траекториям, и потому говорить о траектории движения тела в целом бессмысленно. Однако, можно рассматривать его, как материальную точку, но в этом случае условие абсолютной твёрдости бесполезно.

Человек всегда волен связать с любым движущимся телом систему координат, но характеризуемые ими точки в общем случае будут совершать движения с различными характеристиками.И потому в общем случае говорить о траектории движения материального тела нельзя.Можно говорить лишь о траекториях отдельно выбранных его материальных точек.

Так, например, при вращении тела вокруг постоянной в пространстве оси лишь находящиеся на ней точки будут неподвижны.А одинаковые движение будут совершать лишь те точки, которые находятся на поверхности мысленно выделяемого в теле цилиндра, соосного с осью собственного вращения тела

Некоторые виды пространственных координат

Наиболее употребительными являются декартовы прямоугольные системы координат и сферические системы координат.

Сферическая полярная система координатТакже имеет своей основой декартову систему, но в качестве координат выступают: длина радиуса-вектора $r$ , долгота $\phi$ и полярное расстояние $\vartheta$. При этом долгота измеряется углом поворота проекции радиуса-вектора на плоскость XOY в положительном направлении, а полярное расстояние - угол поворота самого радиуса-вектора от оси OZ.

Декартовы системы координат образованы тремя взаимно пересекающимися в одной точке , называемой началом координат координатными осями. В зависимости от взаимного расположения выбранных за положительное направление, различают правую и левую систему декартовых координат. По умолчанию принята правая система координат, ассоциируемая с правой резьбой или правилом буравчика. А именно положительным направлением оси Z считается такое, по которому движется буравчик, если он совершает поворот от оси X по направлению к оси Y.Это направление вращения считается положительным.В таком случае положение точки задаётся тремя числами, соответствующим проекциям точки (или конца радиуса-вектора) на соответствующие оси.

Иногда положение точки в этой системе координат задают радиусом-вектором, имеющим началом (полюсом) начало системы координат, а конец - в данной точке. Декартова система основана на привычных в повседневной жизни движениях: вперёд-назад, вверх-вниз и вправо-влево и потому настолько популярна, что любое движение по умолчанию считается происходящим именно в этой системе. Если на движение такого материального тела не наложено никаких ограничений, то оно имеет шесть степеней свободы. А именно -три степени свободы его центра масс и три эйлеровых угла. Их находят, совместив с телом координатную систему XYZ, которая в новом положении обозначается , как X’ Y’ Z’ А именно: Угол нутации (выше полярное расстояние $\vartheta$, угол прецессии $\psi$ определяемый как угол между осью OX и следом пересечения OA плоскостей XOYи X’ O Y’так, что прямые OA, OZ, OZ’ образуют тройку правой ориентации и, наконец, угол чистого вращения (правильнее было бы говорить угол чистого поворота, но это не принято ) $\phi$.В соответствие с теоремой вращения Эйлера любой поворот тела имеет ось вращения OZ’.

Значительно реже в качестве такого элементарного физического тела рассматривается 'галтель,представляющая собой тело , имеющее длину, но высоту и ширину настолько малые, что этими размерами можно пренебречь. В качестве таких тел рассматриваются, например, диполи, представляющие собой поляризованные молекулы. Такие тела считаются не имеющими чистого вращения и потому обладающими пятью степенями свободы.

Рис А.Декартовы системы координат

.

На Рис А изображены две декартовы системы координат, позволяющие не только описать движение материальной точки в заданной системе координат, но и выявить зависимость этого движения от выбора системы координат.По установившейся традиции система координат $XOY$ считается неподвижной главным образом потому, что тот, от чьего лица ведётся рассмотрение,считает, что эта система неподвижна относительно него самого и потому является "абсолютной". Но, кроме эгоцентрических предпочтений, существует гораздо боле серьёзная причина считать исходную систему неподвижной, поскольку такая система с определёнными оговорками может считаться инерциальной системой.Такая позиция представляет собой индульгенцию против обвинения в том, что в рассмотрении вопроса не учтены силы инерции.

Однако в любом случае случае движение материальной точки $m$ в пространстве может быть описано изменением во времени радиуса-вектора ${\vec {r}}(t)$. Иногда такое движение называют абсолютным. То есть движение тела по отношению к некоторой системе отсчёта, объявленной инерциальной.

Дополнительно вводится другая система отсчёта "штрихованная" $X^{\prime }O^{\prime }Y^{\prime }$, движение начала которой задаётся вектором ${\vec {R}}(t)$.Изменение этого вектора со временем будет называться переносным движением . В данном случае это переносное движение начала отсчёта штрихованной системы.

Положение материальной точки в штрихованной системе будет определяться вектором ${\vec {(}}r^{\prime }(t))$. Изменение его во времени относительно штрихованной системы будет называться относительным движением.

Взаимосвязь между абсолютным и относительным движением задаётся векторным уравнением:

${\vec {r}}(t)$ = ${\vec {R}}(t)$ + ${\vec {(}}r^{\prime }(t))$

Таким образом на рисунке А изображён частный случай относительного движения двух декартовых систем с постоянной во времени пространственной ориентацией осей, то есть случай движения поступательного.Уникальной особенностью такого вида движения является то, что любая точка, неподвижно связанная с этой системой, при любом движении начала отсчёта движется с точностью до сдвига в пространстве по одной и той же траектории с общими для всех точек величинами мгновенного вектора скорости и её производных.

Именно это существенно упрощающее рассмотрение предположение, что переносное ускорение тела в данном случае равно ускорению штрихованной системы и остаётся одинаковым для любого местоположения тела в любой точке этой системы, делает поступательное движение весьма удобным для рассмотрения задач механики.

Иными словами, если возникает необходимость материализовать в виде реального физического объекта тело отсчёта с общей для любой его точки величиной ускорения, то это можно сделать исключительно в случае поступательного движения такого тела.

Физические тела, совершающие иные, не поступательные, движения телами отсчёта в этом смысле не являются, поскольку составляющие их материальные точки совершают в общем случае различные траектории .И потому графическое представление о разнесённых в пространстве радиус-векторов относительного и переносного движения, как это сделано на Рис.А не представляется возможным.

В связи с этим чревато ошибками использование термина "вращающаяся система отсчёта", являющаяся частным случаем испытывающей поворот координатной системы. Поскольку в общем случае всегда будет идти речь о системе, переносное ускорение в которой различно в разных её точках.

Результатом этого станет появление особого вида ускорения, испытываемого движущимся относительно этой координатной системы, а именно кориолисова ускорения

Чрезвычайно распространено изображение проекции точки на плоскость чертежа, за которую общепринято брать плоскость XOY, что значительно повышает наглядность решаемой задачи в этом случае имеют дело с декартовыми системами координат на плоскости и полярными системами координат.

При этом следует учитывать и всегда помнить , что такое упрощение в ряде задач сопровождается полной потерей информации о явлениях, принципиально происходящих в трёхмерном пространстве, в том числе описание которых зависит от выбора правой или левой системы координат.

Многие задачи механики могут быть рассмотрены в двумерном варианте, достоинством которого является наглядность.

Но есть и более глубокие причины особой приверженности авторов к двумерным способам иллюстрации своих сочинений. Исторически ещё Птоломей, пытаясь объяснить специфику движения небесных тел, особенно внешнихпланет, например Марса, совершающего "попятное " движение на небесно сфере, был вынужден использовать геоцентрическую систему координат. Основой этой системы были эпициклы -круговые движения планет вокруг лежащих вне их центров вращения.Характерно, что в представлениях Птоломея все эти движения совершались в одной плоскости. Что впоследствии подтвердилось тем , что в действительности планеты Солнечной системы обращаются вокруг центрального светила -Солнца, по эллиптическим орбитам, лежащим в одной плоскости. А то обстоятельство, что эти орбиты лежат в плоскости эклиптики, стало одним из наиболее веских подтверждений единства в истории образования всех членов Солнечной системы.

Не раньше двух веков тому назад было показано, что движение планет в одной плоскости обусловлено законами природы и являются следствием специфических свойств силы Всемирного тяготения.Долгое время эта сила либо непосредственно, либо в своих проявлениях была внешней силой, с которой преимущественно сталкивался человек в различных жизненных ситуациях.По своему характеру сила тяготения является силой потенциальной, действие которой может быть исчерпывающим образом проиллюстрировано в плоскости, проходящей через тяготеющие друг к другу тела в виде материальных точек.

Более того, и контактные силы, имеющие своё происхождение в явлении взаимодействия неподвижных электрических эарядов, также являются силами потенциальными и потому их проявления могут быть проиллюстрированы чертежами на плоскости.

Положение радикально изменилось в XIX веке, когда были сформулированы законы электродинамики и широко стало использоваться представление об электро-магнитном поле, описать которое стало возможным лишь при использовании представления о трёхмерном пространстве.Такое поле радикально отличается по свойствам от поля потенциального, поскольку является полем соленоидальным.

Так, если в потенциальном поле явления, происходящие в движущихся относительно друг друга систем отсчёта не зависят от скорости их относительного движения, то для соленоидальных полей эта скорость определяет характер протекающих в них физических процессов, связанных с взаимодействием электрических зарядов.

Траектория

Траектория является объектом изучения раздела механики -кинематики, посвящённой рассмотрению геометрии движения тел без учёта их масс и причин, вызывающих это движение, т.е. без учёта действующих на эти тела сил. Стр.281 )

Понятие о траектории в общем случае неприменимо к описанию движения протяжённых в пространстве тел. Поэтому объектом движения при обращении к этому понятию является материальная точка, имеющая максимум три степени свободы.

Траекто́рия есть непрерывная кривая линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве. Можно сказать, что траектория представляет собой след, который был оставлен или будет оставлен материальной точкой при своём движении в пространстве

Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения.Так улица, в начале которой висит знак «кирпич» останется в принципе траекторией возможного движения по ней.

Тропинка в лесу, или же строчки книги говорят о пути,проходимого пешеходом или о скольжении равнодушного взгляда читателя.

Для конкретного движущегося тела реальна лишь та часть пути, которая уже пройдена, т.е. относится к прошедшему времени. Форма пути, т.е. та часть траектории, которую предстоит преодолеть, может быть предсказана лишь с той или иной степенью вероятности, зависящей от не всегда учтённых факторов.

Если речь идёт о движении материальной точки в пространстве , то её положение в данный момент времени не может быть описано иначе, как по отношению к заданной системе координат в трёхмерном пространстве, а её перемещение - как изменение этих координат во времени.Так, например, векторное уравнение ${\vec {r}}={\vec {r}}(t)$ представляет собой закон движения геометрической точки в его векторном описании.

Время считается единым во всех точках пространства, независимо от расстояния между ними.

Исключив из этого уравнения время $t$ можно получить годограф точки или её траекторию.( Стр. 282)

Таким образом траектория представляет собой пространственную фигуру , образованную следом прошлого или будущего движения, форма которой есть, так сказать, "вещь в себе" в том смысле, что эта форма не зависит от ракурса, под которым она рассматривается.Так форма монеты,представляющей собой диск остаётся диском даже если смотреть на неё с ребра.

Так, например, инверсионный след, оставленный самолётом или же трек , оставляемый частицей в камере Вильсона, несёт в себе однозначную информацию об совершённых ими эволюциях.

Особенно наглядны в этом смысле снимки следов атомных частиц, полученные в толстослойных фотоэмульсиях. Такие снимки можно рассматривать под разным углами, но форма трека частицы по отношению "самой к себе" остаётся, понятно, неизменной.

Вот муха летает по непредсказуемому пути. Но потому и считается, что её полёт не является детерминированным.В случае же детерминированного движения можно говорить о существовании в едином трёхмерном пространстве единственной траектории перемещения в нём тела .Для происшедшего движения в прошлом о форме траектории можно говорить со 100% вероятностью, а о движении происходящем или предстоящем - с той вероятностью, с которой мы можем предсказать эффект от обуславливающих движение факторов. Примерно в этом смысле говорят о собственном движении тела, являющегося объектом наблюдения.

В ряде случаев оказывается возможным представить траекторию в виде материального объекта –канализационной трубы, туманного трека частицы в камере Вильсона или же рельсового пути.Особенностью всех этих вариантов пространственной фиксации ( можно сказать - материализации) траектории является то обстоятельство, что здесь целью является не описание действительно происходящего движения, но лишь указание на его принципиальную возможность.

Сантехник, изгибая применительно к конфигурации помещения канализационную трубу, однозначно определяет траекторию , которой в будущем будут следовать частицы воды.Также и кишечник нашего читателя предопределяет будущее движение внутри тела съеденного бутерброда.И это движение будет происходить по одной и той же траектории, независимо от того , стоит ли человек, бодрствуя или же спит лёжа.

Здесь самое время вспомнить об экспериментах, проделанных ещё в гимназические годы Обертом, который ел яблоко, вися вниз головой. Успех этого нехитрого опыта показал, что траектория частиц съеденного яблока не зависела от ориентации тела в пространстве и в немалой степени во многом укрепил его в мысли о принципиальной возможности для организма человека преодолеть связанные с физиологией проблемы, которые могли бы сделать космический полёт невозможным. , ,

Общим для всех этих примеров является то, что любые объекты, входящие в состав Вселенной существуют , движутся и взаимодействуют совершенно независимо от того , введена ли та или другая , или вообще не введена никакая система отсчёта.

Траектория является пространственной фигурой, форма которой не зависит от наблюдателя. Эта форма связана с пространственной конфигурацией действующих на материальную точку конкретных сил и именно эта конфигурация однозначно определяет ту систему координат, в которой и наблюдается "истинная" траектория.

Но кинематика не занимается анализом причин возникновения того, или иного вида движения. Здесь наблюдатель всегда, подчас несознательно, производит отображение "истинной" траектории в некоторую, избранную им по своим соображениям координатную систему и получает кажущееся, нередко искажённое представление о форме траектории. В этом случае приходится иметь дело с кажущейся траекторией.

С материалистической точки зрения все материальные объекты существуют и движутся в едином и единственном трёхмерном пространстве. Существование других пространств, в которых существовали бы реальные материальные объекты, современной наукой, по крайней мере классической физикой, отрицается.

И для каждого момента времени их расстояние друг от друга имеет совершенно определённое значение, независимо от выбора систем координат, в которых измеряются эти расстояния.Даже самые далёкие,но ещё доступные наблюдению объекты занимают совершенно определённое положение в этом пространстве и разница состоит лишь в том,что ввиду конечной скорости прихода сигнала от них, их сегодняшнее положение соответствует такому, в которых они находились миллионы лет тому назад.

Кстати, последнее уточнение говорит и о том, что идея об общем времени, едином для всех объектов Вселенной не оставлена и в наше время. Иначе вряд ли можно было бы говорить о возрасте Вселенной в целом и называть, пусть приближённо, время Большого взрыва, за которым последовало и рождение Вселенной и начался общий для неё отсчёт времени.

Но, хотя для каждого момента времени взаимное расположение объектов может оказаться другим, новая их пространственная конфигурация в связи со сменой координатной системы также устанавливается однозначно.(При этом привлекается математический аппарат тензорного исчисления). Поэтому и при смене системы координат однозначно и их взаимное движение.Откуда следует утверждение о существовании единственной, соответствующей этому движению траектории в этом единственном реально существующем трёхмерном пространстве.

Изображение туманности Андромеды в УФ лучах

Так, например, изображение удалённой галактики в виде эллипса, могло бы способствовать возникновению заключения, что составляющие её звёзды движутся по эллиптическим траекториям. Хотя на основании иных и достаточно обоснованных положений, астроном склонен считать, что это связано , скорее всего, с проективными искажениями движения по кругу.То есть дело, в том, что мы видим этот небесный объект «с ребра». Конец стрелки часов всегда бежит по кругу, и не потому, что мы это видим. Ведь на циферблат можно посмотреть и под углом. Стрелка бежит так потому, что приводящий её в движение механизм не может придать ей иного движения.

Способы описания траектории

Если считать форму траектории уже известной, то положение точки может быть задано на ней её расстоянием от некоторого начального положения на её траектории.В этом случае имеют дело с естественным или траекторным описанием движения, что может быть представлено графиком на плоскости , где в прямоугольной системе координат по оси абсцисс отложено время, а по оси ординат - расстояние, проходимое точкой в направлении, принятом за положительное, и в этом случае являющееся единственной координатой, описывающей положение точки.(Стр. 282)

В общем виде траектория представляет собой пространственную кривую, свойства которой в каждой точке (за исключением особых точек) на основании положений дифференциальной геометрии кривых описываются сопровождающим трёхгранником , образованным взаимно перпендикулярными единичными векторами. А именно вектором касательной${\vec {t}}$, вектором главной нормали ${\vec {n}}$ и вектором бинормали ${\vec {b}}$ , перпендикулярным так называемой соприкасающейся плоскости, в которой лежат векторы касательной и нормали. Таким образом при своём перемещении по кривой сопровождающий трёхгранник осуществляет поворот вокруг бинормали и кручение в нормальной плоскости, проходящей через нормаль и бинормаль.

И поворот и кручение оцениваются в угловой мере и их производные во времени определяют угловые скорости сложного вращения, результирующая угловая скорость которого представляет собой векторную их сумму.

Траекторию в общем случае можно представить и в виде сопряжённых дуг различного радиуса, исходящих каждая из своего центра, положение которого может меняться во времени. В пределе и прямая может рассматриваться как дуга, радиус которой равен бесконечности

Для моделирования кривых линий с 1962 года используются кривые Безье, описываемые полиномами, степень которых на единицу меньше числа опорных точек.Так, для изображение сегмента любой кривой на плоскости оказывается достаточным указать четыре точки.Этот приём широко используется в инженерной графике, в частности для изображения сложных поверхностей, например, автомобильных кузовов.

Проблема отображения трёхмерных объектов, в том числе и понимаемой в указанном смысле траектории, которую тело имеет «на самом деле», то есть независимо от выбора системы координат, решается в настоящее время, пусть со многими ограничениями, методами голографии.Имеется в виду, что сложная траектория моет быть материализована, например, в виде проволочной пространственной модели. Как это имеет место при проектировании аттракционов типа "американские горы".

Принципиальное значение изобретения и технической реализации технологии создания голографического изображения пространственных объектов состоит в том, что таким образом обеспечена возможность хранения их изображений о многих вариантов их ракурса. То есть без привязки к конкретной системе координат.И это может быть применено и к материализованной указанным выше способом траектории.

В таком случае это позволяет говорить о собственном движении материальных тел, как объективной реальности, не связанной с какой-либо системой пространственных координат. И при том не только в тех условиях, в которых возможно создание голографических изображений, но и вообще в любом другом случае.

То есть речь идёт о придании расширенного смысла этому понятию, которое применяется в астрономии, когда говорят о собственном движении некоторых, ближайших звёзд, обнаруживаемом после исключения годового (параллактического) изменения их координат вследствие движения наблюдателя вместе с Землёй по её орбите.

Человеческий фактор

Проблема ориентации в пространстве и анализа любого в нём перемещения окружающих объектов , то есть проблема адекватной оценки их траектории, является одной из важнейших и жизненно важных проблем, стоящих перед любым представителем животного мира.Но для каждого из них, за исключением некоторой части человеческого сообщества, она решается интуитивно, на основании как врождённых, так и приобретённых инстинктов и рефлексов (условных и безусловных).

Однако, для прогресса человеческого общества оказалось необходимым получение, хранение и использование информации о траектории движения окружающих материальных объектов.

Так, возникла необходимость чётко различать объекты, которые, пусть только на данном отрезке времени, можно считать неподвижными по отношению к другим объектам, движение которых и представляет интерес. Поэтому совершенно естественным образом возникло представление о системе координат, по отношению к которой и происходит движение.

Согласно легенде идея описывать восприятия, получаемые нашими органами чувств числом, пришла в голову Пифагору, обратившего внимание на различие в высоте звуков, издаваемых молотом кузнеца, кующего металлические прутки разной длины. И созданная ещё в античные времена геометрия Евклида обеспечила возможность количественного описания в числах положения тел в пространстве. Воплощением этой идеи стала наиболее популярная в наше время и интуитивно воспринимаемая как естественная прямоугольная система координат Декарта.

Физиологические особенности восприятия информации о внешнем мире , в особенности за счёт зрения (по оценкам обеспечивающего около 80% жизненно необходимой информации) сильно сказались на представлениях об окружающем пространстве. Зрительный аппарат, в основе работы которого лежит отражение трёхмерного мира на поверхности сетчатки глаза , гораздо лучше справляется с оценкой расстояний между предметами в направлении, перпендикулярном направлению взгляда, чем в оценке различия в расстоянии до них.

Оценка же удалённости производится совершено другим физиологическим механизмом (в физиологии зрения это связано с проблемой диспаратности положения изображения на сетчатке левого и правого глаза), точность работы которого существенно уменьшается по мере увеличения дистанции.Поэтому человек склонен отображать предметы на картиной плоскости, т.е вместо оперирования изображением реального мира иметь дело с его проекцией на двумерную плоскость.К тому же изображение , например на листе бумаги, технически гораздо проще, чем трёхмерной модели наблюдаемого.

В некоторой степени, при наличии пространственного воображения, можно создать иллюзию трёхмерного (сейчас говорят 3D) пространства, используя при этом принципы начертательной геометрии (аксонометрия). Но всё равно при этом сохраняется главный недостаток такого описания пространственных объектов, не исключая траекторий, а именно зависимость их формы от выбора системы координат.

Традиционным приёмом, с помощью которого решается вопрос о зависимости траектории от выбора системы координат, является следующий. Вначале постулируется существование некоего наблюдателя, производящего оценку ситуации. Таким наблюдателем в большом числе случаев является сам, занимающийся решением задачи, субъект. Он считает себя неподвижным и связывает с собой свою собственную систему координат. Происходящее в ней движение объекта наблюдения он считает абсолютным.При этом он допускает, что наблюдаемый объект находится в другой, подвижной по отношению к наблюдателю системе координат, по отношению к которой и происходит собственное движение объекта.Для наблюдателя же оно является относительным.Наконец, само движение этой подвижной системы координат относительно своей (абсолютной), наблюдатель называет переносным.

В соответствие с этим собственное движение любой точки на периферии катящегося колеса в виде вращения вокруг его оси в системе, связанной с этой осью для неподвижного наблюдателя является относительным. Перемещение оси в пространстве - переносным, а наблюдаемая траектория точки в форме циклоиды -движением абсолютным. Эдравый смысл говорит, что абсолютным было бы логичнее в данном случае назвать собственное вращение. Но такова традиция, соблюдение которой обеспечивает единообразие описания происходящих явлений. С такой нелогичностью в определениях ещё не раз придётся повстречаться.

И свет, считается что распространяется прямолинейно (известно, что существуют миражи и гравитационные линзы) но это не мешает считать свет распространяющимся прямолинейно и использовать луч лазера для контроля вертикальности московской телебашни , для пространственного монтажа металлоконструкций или проведения прямых линий при малярных работах.

С проблемой прямолинейности столкнулся ещё первобытный охотник, для которого решение этой проблемы при стрельбе из любого оружия, будь то лук или духовая трубка был вопросом его существования. С тех пор эта проблема продолжала существовать на протяжении всей истории человечества.Радикальным шагом, позволившим существенно продвинуться в обеспечении точности прицеливания и поражения цели стало применение гироскопического эффекта при переходе к нарезному огнестрельному оружию. Это -примерно середина XIX (Крымская война). Дальше последовало применение волчка в приборе Обри, обеспечившим прямолинейное движение торпед. А затем и применение гироскопов, основанных на использовании различных эффектов, позволяющих регистрировать ускорения, связанные с отклонением движения снабжённых ими объектов от прямолинейности и равномерности.

Но истинно и то, что в любом случае количественно описать любую кривую можно только в том случае, если априори задаться определённой системой координат . И в этом случае траектория получает конкретное описание языком математики, но с другой сторон теряет свою уникальность потому, что траектория зависит не только от собственного движения тела, но и от пространственной ориентации системы координат и её движения относительно наблюдаемого тела.

Рис.3 Суточное движение светил в системе отсчёта, связанной с фотоаппаратом в проекции на плоскость рисунка

По этой же причине можно дать лишь словесную характеристику собственному движению. При попытке дать ему координатное описание снова возникли бы проблемы, связанные с однозначностью описания ориентации и движения. [[File:|thumb| left| 100 px|]] Как будет показано ниже, возможны ситуации, когда выбором системы координат можно трансформировать прямолинейное собственное движение в криволинейное. И наоборот -криволинейное в прямолинейное. Более того -равномерное движение в ускоренное и ускоренное - в равномерное. Поскольку, вид траектории определяет возможность применения законов механики, произвол, связанный с выбором системы координат ,(зачастую имеющий свое целью лишь увеличения удобства рассмотрения) , сказывается на результатах применения закона. Что приводит к неверному результату..

Убедительный пример этого представляет собой фотоснимок на Рис.3 Здесь изображена полярная область ночного неба, снятая с большой экспозицией. Видно, что все звёзды достаточно большой звёздной величины обращаются, имея поблизости от центра вращения Полярную звезду.Следуя законам механики это можно было бы объяснить наличием центростремительной силы, исходящей из района Полярной звезды.Что неверно в корне.В мировом пространстве не наблюдается вообще явно изображённого на снимке вращения, да ещё с такой невероятно большой угловой скоростью.И эта ошибка вызвана тем, что для регистрации картины звёздного неба выбрана вращающаяся вместе с Землёй фотокамера,являющаяся в данной ситуации координатной системой отсчёта.

Траектория в различных системах координат

Кроме того, и при наличии движущегося по ней объекта, траектория, изображаемая в наперёд заданной системе пространственных координат, сама по себе не может ничего определённого сказать в отношении причин его движения, пока не проведён анализ конфигурации поля действующих на него сил в той же координатной системе.

Так поезда разной массы, движущиеся под различными тяговыми усилиями на сцепных крюках локомотивов и потому с разной скоростью, будут двигаться по одной и той же траектории, определяемой формой рельсового пути, налагающего на движение несвободного тела (поезда) конкретные связи, интенсивность которых будет в каждом случае различной.

Не менее существенно, что форма траектории неотрывно связана и зависит от конкретной системы отсчёта, в которой описывается движение.Так, Луна обращается вокруг Земли только в системе отсчёта, связанной с их общим центром гравитации (находится внутри Земного шара). В системе же отсчёта, началом которой является Солнце, Луна обращается вокруг него по той же эллиптической орбите, что и Земля, но с периодическими отклонениями от неё на величину расстояния от Луны до Земли.К тому же движется он неравномерно, обгоняя Землю с максимальной скоростью в полнолуние и начиная отставать в новолуние.

И обе упомянутые формы траектории истинны и оба объяснения их формы на основании правильно проведённого анализа действующих сил справедливы. Но они исключают друг друга, как исключается возможность одновременного рассмотрения при выборе той или иной системы координат.

Возможно наблюдение траектории при неподвижности объекта, но при движении системы отсчёта. Так, при длительной экспозиции эти звёзды представляются движущимися по круговым траекториям. Не каждый решится объяснить это действием центростремительной силы с центром в Полюсе Мира в районе Полярной звезды.

Возможен и случай, когда тело явно движется, но траектория в проекции на плоскость наблюдения является одной неподвижной точкой. Это, например, случай летящей прямо в глаз наблюдателя пули или уходящего от него поезда.

Как пример, рассмотрим работника театра, передвигающегося в колосниковом пространстве над сценой по отношению к зданию театра равномерно и прямолинейно и несущего над равномерно вращающейся сценой дырявое ведро с краской. Из которого через равные промежутки времени падают капли краски. Они будут оставлять на ней сцене след от падающей краски в форме раскручивающейся спирали (если движется от центра вращения сцены) и закручивающейся — в противоположном случае. Существенно, что по при этом расстояние между следами капель будет увеличиваться, несмотря на постоянство вращения сцены.

В это время его коллега, отвечающий за чистоту вращающейся сцены и на ней находящийся, будет вынужден нести под первым недырявое ведро, постоянно находясь под первым. И его движение по отношению к зданию также будет равномерным и прямолинейным, хотя по отношению к сцене, которая является неинерциальной системой, его движение будет искривлённым и неравномерным . Более того, для того, чтобы противодействовать сносу в направлении вращения, он должен мышечным усилием преодолевать действие силы Кориолиса, которое не испытывает его верхний коллега над сценой, хотя траектории обоих в инерциальной системе здания театра будут представлять прямые линии.

Рис.3

Если бы краска истекала равномерно, то эффект принимал бы в первом приближении вид, изображённый на Рис.3.Неточность состояла бы в том, что по мере приближения к периферии, ширина следа постоянно бы уменьшалась.Что отражало бы влияние нарастающей линейной скорости движения сцены.Возможно, рисование траектории линией различной толщины есть способ, хоть как-то отразить на виде траектории неравномерность движения материальной точки.

Но можно себе представить, что задачей рассматривающихся здесь коллег является именно нанесение прямой линии на вращающейся сцене. В этом случае нижний должен потребовать от верхнего движения по кривой, являющейся зеркальным отражением следа от ранее пролитой краски,оставаясь при этом над любой точкой прямой, проходящей в избранном радиальном направлении. Следовательно, прямолинейное движение в неинерциальной системе отсчёта не будет являться таковым для наблюдателя в инерциальной системе. Более того, равномерное движение тела в одной системе, может быть неравномерным в другой. Так, две капли краски, упавшие в разные моменты времени из дырявого ведра, как в собственной системе отсчёта, так и в системе неподвижного по отношению к зданию нижнего коллеги (на уже прекратившей вращение сцене), будут двигаться по прямой (к центру Земли). Различие будет заключаться в том, что для нижнего наблюдателя это движение будет ускоренным, а для верхнего его коллеги, если он, оступившись, будет падать, двигаясь вместе с любой из капель, расстояние между каплями будет увеличиваться пропорционально первой степени времени, то есть взаимное движение капель и их наблюдателя в его ускоренной системе координат будет равномерным со скоростью , определяемой задержкой между моментами падения капель:

Поэтому форма траектории и скорость движения по ней тела, рассматриваемая в некоторой системе отсчёта, о которой заранее ничего не известно, не даёт однозначного представления о силах, действующих на тело. Решить вопрос о том, является ли эта система в достаточной степени инерциальной, можно лишь на основе анализа причин возникновения действующих сил.

По традиции принято по умолчанию рассматривать движение тела в ИСО. Тогда, если тело движется с непостоянной скоростью, как вектором ,( в том числе меняет направление, т.е. движется по криволинейной траектории), причиной этого считается не уравновешенное взаимное действие на него сил.

Обратное утверждение справедливо не всегда. Тело может находиться в состоянии относительного равновесия, т.е. быть неподвижным в избранной системе координат, которая не инерциальна (неинерциальная система координат - НСО). Примером тому является любой неподвижный материальный объект, принимающий участие во вращении Земного шара. Его неподвижность определяется балансом действующих на него сил: центростремительной, созданной силой гравитации и силой реакцией опоры - с одной стороны и центробежной силой инерции-с другой.( стр.159)

Поступательное движение

Специфическим видом движения тела является так называемое Поступательное движение — механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени, при котором любая прямая, соединяющая любые две точки пространства перемещается параллельно самой себе.

В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе,(что находит своё выражение в сохранении постоянства Эйлеровых углов) остаётся в силе

Рис.1 Пример Трёхмерного поступательного движения тела

В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе,(что находит своё выражение в сохранении постоянства Эйлеровых углов) остаётся в силе.

Математически поступательное движение по своему конечному результату эквивалентно параллельному переносу. Однако, рассматриваемое как физический процесс оно представляет собой в трёхмерном пространстве вариант винтового движения (См. Рис. 1)

В литературе по физике укоренилось представление о том, что поступательное движение есть альтернатива движению вращательному. Такое утверждение содержится, например, в энциклопедии ( страница 282.).Так, например, плоскопараллельное движение твёрдого тела рассматривается как сумма поступательного и вращательного движений . Вместе с тем на другой странице того же издания (Стр.212 - 213)признаётся, что поступательное движение на плоскости может рассматриваться как сумма двух разнонаправленных вращений вокруг двух разных, но взаимно параллельных осей.

Примером реализации такого поступательного движения является движение в координатной системе, связанной с велосипедом,велосипедной педали, состоящего во вращении её вокруг своей оси (относительное движение) и вращении в обратную сторону с той же угловой скоростью шатуна (переносное движение),ось вращения которого укреплена на раме велосипеда и на котором укреплена ось педали.Здесь вращение вокруг собственной оси и одновременное вращение с той же угловой скоростью в обратном направлении вокруг точки вне тела образуют перенос, то есть поступательное движение.

Существенно, что поступательное движение есть единственная разновидность движения трёхмерного тела, когда можно говорить о его траектории, поскольку все его точки движутся по одинаковым (при наложении совпадающим ) траекториям. Более того, только при таком движении тела можно говорить о его скорости и ускорении.Во всех остальных случаях эти понятия для пространственного тела теряют смысл.

Если тело движется поступательно, то для описания его движения достаточно описать движение произвольной его точки (например, движение центра масс тела)и вращательного движения самого тела вокруг центра масс (это обстоятельство принято во внимание при формулировке теоремы Кёнига.

По определению вращение есть такое движение тела, при котором остаётся неподвижной по крайней мере одна точка тела.При поступательном движении таких точек нет, и все точки тела меняют своё положение в пространстве. Разница между поступательным движением и вращением налицо.

Рис 2.Поступательное движение тела на плоскости слева-направо, с произвольно выделенным в нём отрезком AB. Вначале прямолинейное, затем — криволинейное, переходящее во вращение каждой точки вокруг своего центра с равными для данного момента угловыми скоростями и равными значениями радиуса поворота. Точки O — мгновенные центры поворота вправо. R — их равные для каждого конца отрезка, но различные для разных моментов времени мгновенные радиусы поворота.

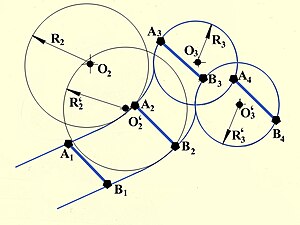
Соль же ясно, что этот пример, приведённый на Рис.2 также не даёт оснований рассматривать поступательное движение как альтернативу вращательному, поскольку в общем виде это движение включает в себя и повороты, и вращение.По-видимому, правильнее различать движения на движение с вращением и движение без такового. Причём повод для различия следует искать в том, испытывает ли тело действие центростремительного ускорения, или нет.

Однако, поступательное движение ни в коем случае не может служить аналогом движения инерциальной системы, что многократно растиражировано литературой по физике, в том числе в массовых учебниках, поскольку в общем случае оно происходит и в условиях, когда тело испытывает поворот, что может иметь место исключительно в системе неинерциальной.И это представляет собой наглядный пример того, как осторожно надо подходить к выяснению смысла используемых в них фундаментальных понятий

При этом подразумевается, что прямолинейное движение есть поворот вокруг бесконечно удалённого от тела центр поворота|центра поворота.Оказывается, что при поступательном движении в каждый заданный момент времени любая точка тела совершает поворот вокруг своего мгновенного центра поворота, причём длина радиуса в данный момент одинакова для всех точек тела. Одинаковы по величине и направлению и векторы скорости точек тела, а также испытываемые ими ускорения.

В случае, когда геометрическими размерами материального тела пренебречь по условиям задачи нельзя, его рассматривают как совокупность материальных точек.Что имеет смысл, например, в небесной механике по отношению к Солнечной системе, где в ряде случаев не только планеты, но и само Солнце рассматриваются как материальные точки.

Скорость

Скорость есть кинематическая величина, определяющая время, в течение которого материальная точка проходит заданное расстояние .Поскольку при неравномерном движении равные расстояния проходятся за разное время, и потому скорость зависит от времени., применяется дифференциальная формула, рассматриваемая как определение понятия "мгновенная скорость", то есть скорость, которую имело быы материальная точка, если бы она с данного момента времени двигалась бы равномерно:

$v(t)=(\partial s)/(\partial t)$

Здесь $v(t)$ есть мгновенная скорость, $\partial s$ есть дифференциал (приращение)пути, а $\partial t$ есть затраченное время.

Привычка измерять расстояния затраченным на его преодоление временем в эпоху реактивной авиации создала иллюзию сокращения расстояний.Однако результат физического процесса, состоящий в том, что материальная точка переместилась из своего первоначального состояния в точку, удалённую на расстояние $\partial s$ никак от скорости не зависит .

Если в заданной системе координат тело двигалось с постоянной скоростью или находилось в покое, но с какого то момента времени получила приращение скорости, то , как это будет показано ниже,это приращение будет пропорционально времени действия силы, вызвавшей это приращение:

$\partial v=(F/m)\partial t$

То есть в нулевой момент времени значение скорости остаётся тем же.Чего нельзя сказать о о её производных, в том числе первой производной - ускорению.

Ускорение

По установившемуся на сегодня общему мнению все взаимодействия в макромире сводятся к проявлениям полей гравитационного и электромагнитного.Интенсивность этих полей определяется механической силой $F$, действующей на пробный объект.В таком случае интенсивность поля принято называть его напряжённостью.

Для гравитационного поля таким пробным телом объектом является материальное тело, обладающее массой $m$, а напряжённость поля называется ускорением свободного падения $g$:

$g=F/m$

Для электростатического поля, то есть частного вида электромагнитного поля неподвижных по отношению друг к другу зарядов, напряжённость электрического поля$E$ пропорциональна ускорению $a$, порождаемому кулоновской (но также механической) силой $F_{q}$, где коэффициентом пропорциональности служит отношение массы пробного тела к его заряду $q$:

$E=a(m/q)$

Здесь следует обратить внимание на то обстоятельство, что отличающаяся от нуля величина ускорения не обязательно связана с движением.В данном случае электростатическое поле будет существовать и без внесения в него пробного заряжённого объекта. И, соответственно и с известным коэффициентом пропорциональности, такое поле будет вызывать появление ускорения вносимого объекта, причём мгновенно,без задержки в момент его появления в этом поле.

Если же этому объекту будет предоставлена возможность двигаться, то, наряду с электростатическим, возникнет и поле магнитное.Поэтому , наряду с кулоновской силой, появится и поле движущихся относительно зарядов. И сила их взаимодействия будет силой Лоренца, в которой кулоновская сила станет одним из двух слагаемых.

Таким образом с общефизической точки зрения ускорение представляет собой главную характеристику каждого из рассматриваемых в макроскопических масштабах силового поля, являющегося причиной происходящих во времени и пространстве изменений, описываемых кинематикой.Но кинематика вообще не интересуется вопросом о происхождении движения.

По определению, характерному для кинематического подхода, ускорение здесь есть скорость изменения скорости.Так как скорость есть векторная величина, ${\vec {v}}$, то ускорение ${\vec {a}}$ представляет собой тоже вектор:

${\vec {a}}=d{\vec {v}}/dt$

То есть изменение величины и направления вектора скорости в единицу времени $dt$.

Если объектом рассмотрения является материальная точка, то такое определение сразу даёт основание для разделения её ускорения на две составляющие.То есть ускорение, представляющее собой изменение скорости в предположении, что с данного момента точка будет двигаться по прямой линии и ускорения, связанного с изменением направления движения, которое можно рассматривать,как нарушение прямолинейности вследствие поворота.

Хотя и здесь ускорение есть производная от скорости, оно не обязательно должно быть равным нулю при её отсутствии. Так, наибольшее ускорение испытывает груз маятника, когда он достигает крайней точки своего качания. Также и точка на периферии катящегося без проскальзывания колеса испытывает наибольшее ускорение в момент касания с поверхностью качения, когда она оказывается "на мгновение" неподвижной.

Прибором, позволяющим фиксировать наличие и измерять ускорение, является акселерометр. Простейшим и весьма грубым устройством является инерционный акселерометр (См. Рис. ), представляющий собой груз $m$, имеющий возможность смещаться только в одном направлении, который удерживается в неподвижности относительно своего корпуса двумя противоположно действующими на него пружинами. Перед измерением , как это принято при любых измерениях, с помощью проводится установка нуля.

Уже сам факт, что в течение некоторого времени удалось установить ноль, свидетельствует, что по крайней мере в это время объект, ускорение которого предстоит измерять, имел постоянное ускорение в направлении возможного смещения груза.

Если же имеется желание измерять ускорение происходящее в пространстве, следует использовать три акселерометра , ориентированных, например, в направлении трёх декартовых координат системы отсчёта, связанной с объектом.

Пусть противоположно действующие на груз пружины акселерометра выбраны так, что при равных действующих на них силах они испытывают одинаковые деформации .Тогда наблюдаемый факт различного изменения длины пружин будет однозначно свидетельствовать о наличии у прибора ускорения в направлении возможного смещения груза.Если же длины пружин будут одинаковы, то это будет с точностью погрешности измерения этих длин говорить о том, что прибор ускорения не испытывает, то есть находится в квази- инерциальной системе отсчёта. То есть в такой системе, в которой действующие на груз силы, независимо от их происхождения, не превышают погрешности измерения.Это положение груза, отмеченное на шкале, используемой для констатации смещения груза, назовём нулевым положением.Смещение груза вследствие действия на него силы инерции, вызывающей изменение длины пружин, даёт возможность измерить величину проекции вектора ускорения на направление смещения груза. Иными словами величину ускорения прибора в заданном направлении.

Если же теперь принять это положение груза снова за начало отсчёта, то есть выставить шкалу смещения снова на нуль, то смещение груза от этого, нового положения нуля будет указывать на изменение ускорения. В этом случае прибор будет показывать величину относительного по отношению к прежней ситуации ускорения прибора.

Если же положение груза будет во время наблюдения изменяться, то это будет говорить о непостоянстве испытываемого в заданном направлении ускорения, то есть о существовании отличной от нуля второй производной скорости,величина которой может быть установлена через оценку скорости изменения величины ускорения. В любом случае акселерометр покажет изменение ускорения по отношению к тому ускорению, которое он имел в заданном направлении при установке нуля.

Прибор одинаковым образом реагирует как на изменение скорости при прямолинейном движении своего движении, так и при повороте. И даёт информацию о составляющей ускорения в направлении смещения груза, которая в зависимости от предварительной установки нуля .

Заметим, что акселерометр имеет две ипостаси: во-первых, он сам представляет движущийся объект , во вторых, он , как неподвижно связанный с объектом,принятым за систему отсчёта, является её частью.

Следует обратить особое внимание на то, что всё сказанное выше относилось к случаю, когда измеряемое акселерометром ускорение было вызвано силой, на подвижный груз не действующей.

Обратимся теперь к дидактическому приёму, широко используемому при изложении основ механики, в основанных на догматическом подходе к изложению материала, руководствах по физике.А именно рассмотрим инерциальную систему ( понятно,то речь идёт о квази-инерциальной системе), в которой одна за другой по прямой , но с разными скоростями движутся две материальные точки. Волевое утверждение о принятии для рассмотрения инерциальной системы исключает вполне закономерно возникающее подозрение о том, что траектория движения лишь кажется прямолинейной. В самом деле инерциальные системы обладают тем свойством, что прямолинейность любого отрезка сохраняется при переходе от одной системы отсчёта к другой.

Введём уточнение, что скорости движущихся точек отличаются на неизменную величину $V$. То есть, применяя принятое в классической механике правило сложения скоростей, запишем:

$V(t)_{2}-V(t)_{1}=V$

Взяв от обеих частей производную , и помня, что разница в скоростях есть постоянная величина, а производная от скорости есть ускорение, получим, что

$a(t)_{1}=a(t)_{2}$

Из чего следует заявление, что ускорение двух материальных точек , движущихся с неизменной скоростью одна относительно другой и отнесённые к одной и той же инерциальной системе координат, равны.Одинаковые акселерометры, неподвижно связанные с этими точками и выставленные на нуль в инерциальной системе покажу одно и то же ускорение.

Ничто не мешает связать с каждой из материальных точек систему координат, которая в рассматриваемом случае будет по определению неинерциальной.Также ничто не мешает рассматривать любую из этих систем координат, как исходную относительно движения системы координат, связанной с другой точкой. Так, например, получаем, что в системе координат первой точки, вторая движется прямолинейно и равномерно с постоянной скоростью , причём является системой неинерциальной. Что с очевидностью показывает установленный на ней акселерометр.

Из этого следует, что равномерность и прямолинейность движения не является решающим признаком, позволяющим отличить неинерциальную систему от инерциальной. Таким признаком в этом случае является факт наличия у неинерциальной системы ускорения. Или проще: скорость относительна, ускорение же абсолютно и не зависит от характера движения системы отсчёта.

Существенно, что при упомянутой выше процедуре установки начального нуля акселерометра, вообще отсутствует необходимость в совершении этого действия именно в инерциальной системе.Поскольку отметка абсолютного нуля по равенству длин пружин может быть произведена в любой системе отсчёта, как неинерциальной, так и инерциальной.Можно сказать, что при этом происходит моделирование инерциальной системы отсчёта. Точнее - выделение одного из множества её вариантов.