Трапеция

Трапе́ция (от др.-греч. τραπέζιον — «столик» от τράπεζα — «стол») — выпуклый четырёхугольник, у которого только две противолежащие стороны параллельны.

.

Варианты определения

Существует и другое определение трапеции.

Трапеция — это выпуклый четырёхугольник, у которого две стороны параллельны. Согласно этому определению, параллелограмм и прямоугольник — частные случаи трапеции. Однако при использовании такого определения большинство признаков и свойств равнобедренной трапеции перестают быть верными (так как параллелограмм становится её частным случаем). Приведённые в разделе Общие свойства формулы верны для обоих определений трапеции.

Связанные определения

Элементы трапеции

Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой

• Параллельные противоположные стороны называются основаниями трапеции.
• Две другие стороны называются боковыми сторонами.
• Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
• Углом при основании трапеции называется её внутренний угол, образованный основанием с боковой стороной.

Виды трапеций

• Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией (реже равнобокой или равнобочной трапецией).
• Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

• 
  Равнобедренная трапеция
• 
  Прямоугольная трапеция

Свойства

• Средняя линия трапеции параллельна основаниям и равна их полусумме.
• Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
• Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен ${\frac {2xy}{x+y}}$ среднему гармоническому длин оснований трапеции.
• В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
• Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
• Если сумма углов при одном из оснований трапеции равна 90°, то продолжения боковых сторон пересекаются под прямым углом, а отрезок, соединяющий середины оснований, равен полуразности оснований.
• Диагонали трапеции делят её на 4 треугольника. Два из них, прилежащие к основаниям, подобны. Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.
• Если отношение оснований равно $K$, то отношение площадей треугольников, прилежащих к основаниям, равно $K^{2}$.
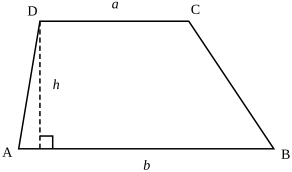
• Высота трапеции определяется формулой:

$h={\sqrt {c^{2}-{\frac {1}{4}}\left({\frac {c^{2}-d^{2}}{b-a}}+b-a\right)^{2}}}$

где $b$ — большее основание, $a$ — меньшее основание, $c$ и $d$ — боковые стороны.

• Диагонали трапеции $d_{1}$ и $d_{2}$ связаны со сторонами соотношением:

$d_{1}^{2}+d_{2}^{2}=2ab+c^{2}+d^{2}$

Их можно выразить в явном виде:

$d_{1}=AC={\sqrt {ab+d^{2}+{\frac {b(c^{2}-d^{2})}{b-a}}}}$

$d_{2}=BD={\sqrt {ab+c^{2}-{\frac {b(c^{2}-d^{2})}{b-a}}}}$

Если, наоборот, известны боковые стороны и диагонали, то основания выражаются формулами:

$a={\sqrt {\frac {(c^{2}-d_{1}^{2})^{2}-(d^{2}-d_{2}^{2})^{2}}{2(c^{2}-d^{2}+d_{1}^{2}-d_{2}^{2})}}}$

$b={\sqrt {\frac {(c^{2}-d_{2}^{2})^{2}-(d^{2}-d_{1}^{2})^{2}}{2(c^{2}-d^{2}-d_{1}^{2}+d_{2}^{2})}}}$

а при известных основаниях и диагоналях боковые стороны следующие:

$c={\sqrt {\frac {a(d_{2}^{2}-b^{2})+b(d_{1}^{2}-a^{2})}{a+b}}}$

$d={\sqrt {\frac {a(d_{1}^{2}-b^{2})+b(d_{2}^{2}-a^{2})}{a+b}}}$

Если же известна высота $h$, то

$d_{1}={\sqrt {b^{2}+d^{2}-2b{\sqrt {d^{2}-h^{2}}}}}={\sqrt {h^{2}+\left(b-{\sqrt {d^{2}-h^{2}}}\right)^{2}}}$

$d_{2}={\sqrt {b^{2}+c^{2}-2b{\sqrt {c^{2}-h^{2}}}}}={\sqrt {h^{2}+\left(b-{\sqrt {c^{2}-h^{2}}}\right)^{2}}}$

• Прямая Ньютона для трапеции совпадает с её средней линией.

Равнобедренная трапеция

Трапеция является равнобедренной тогда и только тогда, когда выполнено любое из следующих эквивалентных условий:

• прямая, которая проходит через середины оснований, перпендикулярна основаниям (то есть является осью симметрии трапеции);
• высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований;
• углы при любом основании равны;
• сумма противоположных углов равна 180°;
• длины диагоналей равны;
• вокруг этой трапеции можно описать окружность;
• вершинами этой трапеции также являются вершины некоторого антипараллелограмма.

Кроме того

• если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная и описанная окружность

• Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
• В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
• Если трапецию можно вписать в окружность — то она равнобедренная.
• Радиус описанной окружности равнобедренной трапеции:

$R={\frac {bcd_{1}}{4{\sqrt {p(p-b)(p-c)(p-d_{1})}}}}={\sqrt {\frac {ab+c^{2}}{4-\left({\frac {b-a}{c}}\right)^{2}}}}$

где $p={\frac {1}{2}}(b+c+d_{1})\,,\,c$ — боковая сторона, $b$ — бо́льшее основание, $a$ — меньшее основание, $d_{1}=d_{2}$ — диагонали равнобедренной трапеции.

• Если $a+b=2c$, то в равнобедренную трапецию можно вписать окружность радиуса

$r={\frac {h}{2}}={\frac {\sqrt {ab}}{2}}$

• Если в трапецию вписана окружность с радиусом $r$, и она делит боковую сторону точкой касания на два отрезка — $v$ и $w$ — то $r={\sqrt {vw}}$.

Площадь

Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.

• В случае, если $a$ и $b$ — основания и $h$ — высота, формула площади:

$S={\frac {(a+b)}{2}}h$

• В случае, если $m$ — средняя линия и $h$ — высота, формула площади:

$S=\displaystyle mh$

Примечание: Приведённые выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:

$m={\frac {(a+b)}{2}}$

• Формула, где $a<b$ — основания, $c$ и $d$ — боковые стороны трапеции:

$S={\frac {a+b}{4(b-a)}}{\sqrt {(a+c+d-b)(a+d-b-c)(a+c-b-d)(b+c+d-a)}}.$

или

$S={\frac {a+b}{2}}{\sqrt {c^{2}-{\frac {1}{4}}\left({\frac {c^{2}-d^{2}}{b-a}}+b-a\right)^{2}}}$

• Средняя линия $m$ разбивает фигуру на две трапеции, площади которых соотносятся как

${\frac {S_{1}}{S_{2}}}={\frac {3a+b}{a+3b}}$

• Площадь равнобедренной трапеции с радиусом вписанной окружности, равным $r$, и углом при основании $\alpha$:

$S={\frac {4r^{2}}{\sin {\alpha }}}$

• Площадь равнобедренной трапеции:

$S=(b-c\cos {\gamma })c\sin {\gamma }=(a+c\cos {\gamma })c\sin {\gamma }$

где $c$ — боковая сторона, $b$ — бо́льшее основание, $a$ — меньшее основание, $\gamma$ — угол между бо́льшим основанием и боковой стороной.

• Площадь равнобедренной трапеции через её стороны

$S={\frac {a+b}{2}}{\sqrt {c^{2}-{\frac {1}{4}}(b-a)^{2}}}$

• Площадь трапеции равна произведению одной из боковых сторон на длину перпендикуляра, проведённого из середины другой боковой стороны к прямой, содержащей первую боковую сторону.

История

Слово «трапеция» происходит от греческого слова др.-греч. τραπέζιον «столик» (уменьш. от τράπεζα «стол»), означающего стол. В русском языке от этого слова происходит слово «трапеза» (еда).

Песочница — Как писать учебники и руководства — Список правил и руководств — Общий форум — Технический раздел — Планы и заявки — Голосования  Удаление страниц — Восстановление страниц — Переименование страниц — Разделение страниц — Объединение страниц Запросы к администраторам — Форум администраторов — Выборы администраторов