Построение разверток тел вращения
Окружающий нас мир динамичен и разнообразен, и далеко не всякий объект можно просто обмерить линейкой. Для подобного переноса используются специальные техники, как то триангуляция.
Потребность в составлении сложных развёрток, как правило, возникает при моделировании, работе с бумагой и металлом, в слесарном деле. Написанная ниже статья, объясняет принципы построения развёрток тел вращения (цилиндр, конус) и их частных случаев (сечение конуса, конус с переходом с круга на квадрат).
Основы и инструмент
[править]- Все нижеописанные действия выполняются на бумаге, при помощи линейки, карандаша и циркуля. Рекомендуется комплект лекал, для повышения точности и качества развёрток.
- При изготовлении развёрток на металле используется метровая линейка, чертилка, циркуль по металлу, комплект лекал, молоток и керно, для отметки узловых точек.
- Длина окружности считается по формуле:
или
Где:
— радиус окружности,
— диаметр окружности,
— длина окружности,
— Число Пи (Pi),
Как правило, для вычисления используется значение (Pi) до второго знака (3,14), но в некоторых случаях, этого может быть недостаточно.
- Усечённый конус с доступной вершиной: Конус, при построении которого можно определить положение вершины.
- Усечённый конус с недоступной вершиной: Конус, при построении которого положение вершины определить затруднительно, в виду её удалённости.
- Триангуляция: способ построения разверток поверхностей неразвертывающихся, конических, общего вида и с ребром возврата.
- Восстановление размера: Многие размеры трёхмерного объекта, при проецировании в двумерную плоскость, оказываются мнимыми, поэтому их приходится восстанавливать по правилу треугольника: «Если известны две стороны — то можно получить третью». В этих случаях применяется прямая, с вертикалью, верхняя точка вертикали соответствует высоте объекта. Если из точки пересечения (на нижеследующих чертежах — точка O) отложить на прямой размер снятый с вида сверху — то размер из полученной из точки до вершины вертикали (на нижеследующих чертежах — точка O1) - является истинным.
- Следует помнить: Независимо от того, является рассматриваемая поверхность развертываемой или неразвертываемой, графически может быть построена только приближенная развертка. Это объясняется тем, что в процессе снятия и откладывания размеров и выполнения других графических операций неизбежны погрешности, обусловливаемые конструктивными особенностями чертежных инструментов, физическими возможностями глаза и погрешностями от замены дуг хордами и углов на поверхности плоскими углами. Приближенные развертки кривых не-развертывающихся поверхностей, кроме графических погрешностей, содержат погрешности, полученные за счет несовпадения элементов таких поверхностей с плоскими аппроксимирующими элементами. Поэтому для получения поверхности из такой развертки, кроме изгибания, необходимо произвести частичное растяжение и сжатие отдельных ее участков. Приближенные развертки при тщательном выполнении обладают точностью, достаточной для практических целей.
Представленный в статье материал, подразумевает, что вы имеете представление об основах черчения, умеете делить окружность, находить центр отрезка при помощи циркуля, снимать/переносить размеры циркулем, пользоваться лекалами, и соответствующим справочным материалом. Потому, объяснение многих моментов в статье опущено.
Построение развёртки цилиндра
[править]Построение развёртки конуса
[править]Конус с квадратным (многогранным) основанием.
[править]
- В случае, если конус имеет ровное, радиальное, основание: (При построении окружности на виде с верху, путём установки циркуля в центр, и очерчивания окружности по произвольной вершине — все вершины основания укладываются на дугу окружности.) Построить конус, по аналогии с развёрткой обычного конуса (основание строить по окружности, от вида сверху). Отложить дугу из точки O. В произвольной части дуги поставить точку A1, и поочерёдно отложить все грани основания на дугу. Конечная точка последней грани будет B1.
- Во всех иных случаях конус строится по принципу триангуляции, с поочерёдным восстановлением высот от вида сверху.
Усечённый конус с доступной вершиной
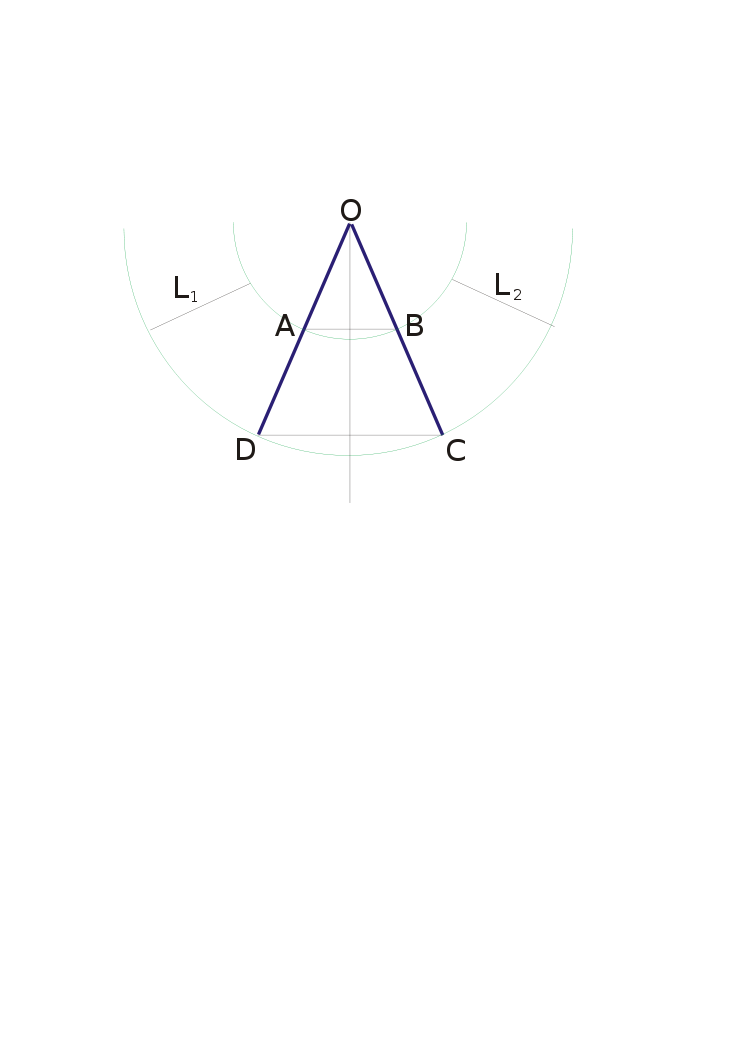
[править]Построить усечённый конус ABCD в натуральную величину (См. чертёж).
Стороны AD и BC продолжить до появления точки пересечения O. Из точки пересечения O, провести дуги, с радиусом OB и OC.
На дуге OC, отложить длину окружности DC. На дуге OB, отложить длину окружности AB. Полученные точки соединить отрезками L1 и L2.
Для удобства, от можно откладывать половину длины окружности, в обе стороны от осевой линии конуса.
Как отложить длину окружности на дуге:
- При помощи нитки, длина которой равна длине окружности.
- При помощи металической линейки, которую следует изогнуть «по дуге», и поставить соответствующие риски.
- Построить окружность основания конуса в виде сверху, в натуральную величину. Разделить окружность на 12 или более равных частей, и отложить их на дуге поочерёдно.
Примечание: Совсем не обязательно, что отрезки L1 и L2, если их продолжить, будут сходится в точке O. Если быть до конца честным, то сойтись они должны, но с учётом поправок на погрешности инструмента, материала и глазомера — точка пересечения может оказаться чуть ниже или выше вершины, что не является ошибкой.
Усечённый конус с недоступной вершиной
[править]Строится так же, как усечённый конус со смещёнными основаниями.
Усечённый конус с переходом с круга на квадрат
[править]Подготовка:
Построить усечённый конус ABCD в натуральную величину (см. чертёж), построить вид сверху ABB1A1. Окружность поделить на равные части (в приведённом примере показано деление одной четверти). Точки AA1-AA4 соединить отрезками с точкой A. Провести ось O, из центра которой провести перпендикуляр O-O1, высотой равной высоте конуса.
Ниже, первичные размеры снимаются с вида сверху.
Построение:
- Снять размер AD и построить произвольную вертикаль AA0-AA1. Снять размер AA0-A, и поставить «примерную точку», сделав отмашку циркулем. Снять размер A-AA1, и на оси O, из точки O, отложить отрезок, снять размер из полученной точки до точки O1. Сделать отмашку циркулем из точки AA1, до предполагаемой точки A. Соединить отрезками точки AA0-A-AA1.
- Снять размер AA1-AA2, из точки AA1 поставить «примерную точку», сделав отмашку циркулем. Снять размер A-AA2, и на оси O, из точки O, отложить отрезок, снять размер из полученной точки до точки O1. Сделать отмашку циркулем из точки A, до предполагаемой точки AA2. Провести отрезок A-AA2. Повторить, пока не будет отложен отрезок A-AA4.
- Снять размер A-AA5, из точки A поставить «примерную точку» AA5. Снять размер AA4-AA5, и на оси O, из точки O, отложить отрезок, снять размер из полученной точки до точки O1. Сделать отмашку циркулем из точки AA4, до предполагаемой точки AA5. Провести отрезок AA4-AA5.
Подобным образом построить остальные сегменты.
Примечание: Если конус имеет доступную вершину, и КВАДРАТНОЕ основание - то построение можно провести по принципу усечённого конуса с доступной вершиной, а основание — конуса с прямоугольным (многогранным) основанием. Точность будет ниже, но построение существенно проще.
Усечённый конус с непараллельными основаниями
[править]Усечённый конус со смещёнными основаниями
[править]Подготовка:
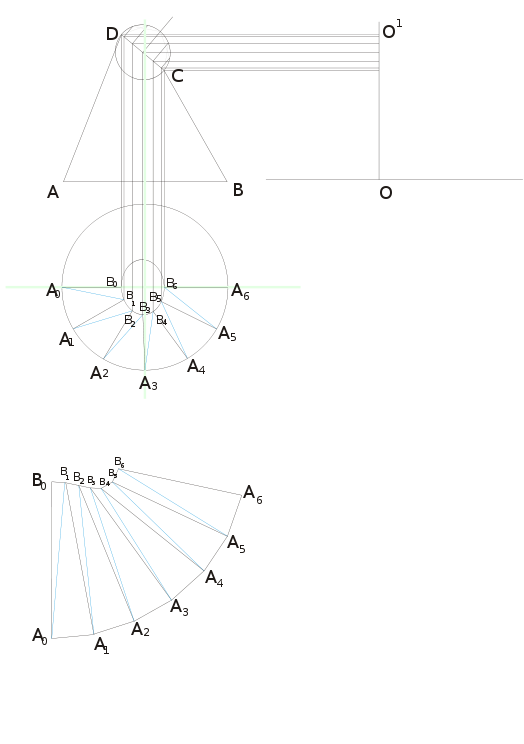
Построить усечённый конус ABCD в виде сбоку, в натуральную величину. Построить вид сверху (см.чертёж). Поделить верхнее и нижнее основание на равные части A0-6 и B0-6, соединив соответствующие точки отрезками. Построить вспомогательные диагонали (на чертеже выделены синим цветом). Провести ось O, из центра которой провести перпендикуляр O-O1, высотой равной высоте конуса.
Ниже, первичные размеры снимаются с вида сверху.
Построение:
- Построить вертикаль A0-B0. (В рассматриваемом случае, верхняя плоскость смещена влево так, что точки A и D находятся на одной вертикали. Поэтому размер AD, соответствующий размеру A0-B0 снимается с вида с боку. В иных случаях он получается восстановлением размера на оси O.)
- Снять размер A0-A1. Из точки A0, вертикали A0-B0, сделать примерную отмашку циркулем. Снять размер B0-B1. Из точки B0, вертикали A0-B0, сделать примерную отмашку циркулем. Снять размер вспомогательной диагонали A0-B1, из точки O, сделать отмашку циркулем на ось, из полученной точки снять размер до точки O1, полученным размером сделать отмашку из точки A0, для получения точки B1.
- Снять размер A1-B1, из точки O, сделать отмашку циркулем на ось, из полученной точки снять размер до точки O1, полученным размером сделать отмашку из точки B1, для получения точки A1.
- Соединить отрезками точки A0-B0-B1-A1.
Аналогичным образом продолжить построение до получения половины, либо цельной развёртки.
Обобщения и замечания
[править]- Используя вышеприведённую технику, можно построить развёртку практически любого объекта со сложной топографией.
- При этом следует иметь в виду, что при работе с металлом следует брать внутренние размеры детали, т.к. при гибке и/или закатке, внешняя поверхность металла тянется, а внутренняя остаётся неизменной. (Верно при использовании современного гибочного оборудования. На устаревшем оборудовании, следует вводить поправки на износ поверхностей, и точность работы станка.)
- При работе с металлом, толщиной свыше 3 мм, в зависимости от типа, марки металла и используемого гибочного оборудования - размеры следует брать не по внутренней стороне, а по «средней линии», которая проходит на половине толщины металла. Либо считать места сгибов не как прямые углы, а как дуги.
- При изготовлении из металла, линии разметки (прямые, а не вспомогательные диагонали) могут использоваться как линии гиба, с последующей доводкой контура молотком/киянкой на вспомогательной поверхности.
См. также
[править]- ГОСТ 2.301-68* Форматы. (размеры форматов и их обозначение)
- Начертательная геометрия и черчение.Книга начертательная геометрия и машиностроительное черчение. Под редакцией Чекмарева А.А.
- Справочное руководство по черчению. Под редакцией Е.И. Годик и А.М. Хаскин. Москва "МАШИНОСТРОЕНИЕ" 1974г.
- ЧЕРЧЕНИЕ. Под редакцией Боголюбова С.К. Учебник для средних специальных учебных заведений (2-е изд.)