Понятие о помехах и методы борьбы с ними
Помехи: понятие и характеристики
[править]Помехой называется стороннее возмущение, действующее в системе передачи и препятствующее правильному приёму сигналов.
Источники помех могут находиться как вне, так и внутри самой системы передачи.
Если помеха регулярна и известна, то борьба с ней не представляет затруднений. Например, фон переменного тока может быть устранён компенсацией; помеха от определенной радиостанции с модуляционным спектром нормальной ширины устраняется соответствующим фильтром. Борьба же со случайными помехами представляет наибольшее затруднение.
В общем виде влияние помехи на передаваемый сигнал может быть выражено оператором
В том частном случае, когда этот оператор вырождается в сумму
помеха называется аддитивной. Аддитивную помеху часто называют шумом.
Если же может быть представлен в виде
где случайный процесс (см. ниже) неотрицателен, то помеху называют мультипликативной. Если — медленный (по сравнению с ) процесс, то явление, вызываемое мультипликативной помехой, носит название замирание (фединг).
В более общем случае оператор не может быть приведён к основным формам (2) и (3). При одновременном наличии шума и мультипликативной помехи удобно ввести два случайных процесса, выражающих оба вида помехи:
С физической точки зрения случайные помехи порождаются различного рода флуктуациями. Флуктуациями в физике называют случайные отклонения тех или иных физических величин от их средних значений. Так, источником шума в электрических цепях постоянного тока могут являться флуктуации тока около среднего значения, обусловленные дискретной природой носителей заряда (ионов и электронов). Это явление носит название дробового эффекта.
Наиболее универсальной причиной шума являются флуктуации, обусловленные тепловым движением. Случайное тепловое движение носителей заряда в любом проводнике вызывает случайную разность потенциалов на его концах. Эта разность потенциалов флуктуирует около среднего значения, равного нулю; её средний квадрат пропорционален абсолютной температуре. Возникающая помеха называется тепловым шумом.
Из сказанного видно, что флуктуации и обусловленные ими помехи заложены глубоко в природе вещей.
Флуктуации есть результат дискретного строения вещества и статистической природы ряда физических величин. Многие физические величины представляют результат усреднения по большому числу индивидуальных частиц, поведение и действие которых подчиняется законам случая. Поэтому флуктуации этих физических величин принципиально неустранимы, и можно лишь ставить вопрос о том, какова относительная величина флуктуации и каким образом мы можем на неё повлиять находящимися в нашем распоряжении средствами.
Имеется ещё один источник принципиально неустранимого шума, возникающего из-за дискретной природы электромагнитного излучения. Согласно современным воззрениям излучение совершается дискретными порциями — квантами, энергия которых равна , где — постоянная Планка, — частота. Квант электромагнитного излучения называется фотоном. В настоящее время в технике имеются две ясные тенденции: к увеличению расстояний и к повышению частоты. Увеличение расстояний означает уменьшение потока энергии, а повышение частоты — укрупнение фотонов. Таким образом, при определённых условиях не только начинает ощущаться дискретная фотонная структура излучения, но обусловленный этой причиной шум может превзойти все остальные помехи. Канал, работающий при таких условиях, получил название фотонного канала.
Выше перечисленные шумы являются аддитивными, но имеется обширный класс мультипликативных помех.
Природа этих помех состоит в случайном изменении параметров канала передачи. При передаче сигнал подвергается искажениям вследствие того, что коэффициент передачи канала не является постоянным числом; свойства канала описываются частотными или временны́ми характеристиками, определяющими так называемые линейные искажения. Кроме того, канал может вносить и нелинейные искажения, обусловленные нелинейностью тех или иных звеньев канала.
Как линейные, так и нелинейные искажения обусловлены известными характеристиками канала, а потому, по крайней мере в принципе, могут быть устранены путем надлежащей коррекции. Поэтому искажения следует чётко отделить от действия помехи случайного характера, которая заранее не может быть известна.
Если же коэффициент передачи канала претерпевает случайные изменения, то влияние этих изменений следует уже рассматривать как действие случайной помехи, которая и является мультипликативной помехой.
Примером медленной мультипликативной помехи является изменение силы принимаемого сигнала, обусловленное интерференцией при многолучевом распространении (замирание). Быстрая мультипликативная помеха возникает при использовании шума в качестве переносчика.[1]
Помеха представляется случайной функцией времени. Случайную функцию дискретного времени называют случайной последовательностью, случайную функцию непрерывного времени — случайным процессом. Случайные функции характеризуются своими распределениями. Применяются также числовые характеристики в виде моментов распределения. Обычно рассматриваются стационарные случайные процессы.
Важнейшей характеристикой канала с аддитивной помехой является отношение средних мощностей сигнала и помехи
Это отношение, кратко называемое отношение «сигнал/помеха», играет большую роль в теории помехоустойчивости.
На практике отношение «сигнал/помеха» выражают в логарифмических безразмерных единицах — децибелах (dB, дБ):
Случайные процессы характеризуются определённым набором показателей.
Момент первого порядка (первый момент)
выражает математическое ожидание, или постоянную составляющую процесса.
Центральный момент второго порядка (второй момент) называется дисперсией и равен:
Дисперсия выражает мощность переменной составляющей, а средний квадрат — общую мощность. В большинстве случаев , так что дисперсия совпадает со средним квадратом.
Смешанный второй момент
называется функцией автокорреляций процесса . Величина есть мощность процесса. Действительно
Многие случайные процессы, встречающиеся в практике, обладают свойством эргодичности. Это свойство состоит в том, что средние по множеству (то есть математические ожидания, вычисляемые по распределениям) с вероятностью единица совпадают со средними по времени, найденными по одной реализации процесса. Тогда для эргодических процессов имеем
Спектральная плотность мощности (или просто спектр) связана с функцией автокорреляции парой преобразований Фурье:
Положив во второй формуле , получим соотношение, поясняющее смысл функции :
Наряду с часто пользуются функцией — мощность, приходящаяся на полосу 1 Гц. Поэтому удобнее записать (12) в виде
Задание исчерпывающим образом характеризует любой случайный процесс.
Некоторые виды шумов
[править]Гауссов шум
[править]Среди всех случайных процессов особое место занимает процесс с нормальным распределением (гауссов процесс). Дело в том, что большое число действительных случайных процессов является гауссовыми. Это обстоятельство находит себе объяснение в известной теореме Ляпунова, согласно которой распределение суммы независимых случайных величин (при некоторых достаточно широких условиях) сходится к нормальному, вне зависимости от характера распределения слагаемых.
Гауссов шум, или гауссов случайный процесс, возникает при суммировании статистически независимых белых шумов (см. ниже). Он преобладает в практических задачах. Случайный процесс называется гауссовым, если для любого набора фиксированных моментов времени случайные величины подчиняются нормальному распределению. Плотность вероятностей мгновенных значений гауссова процесса определяется выражением:
где — среднее значение;
— стандартное (среднеквадратичное) отклонение.
Среднее значение для гауссова распределения равно математическому ожиданию:
Стандартное (среднеквадратичное) отклонение:

Следовательно, плотность вероятностей гауссова процесса полностью характеризуется спектральной плотностью, по которой можно определить значение дисперсии процесса. На рисунке 1 показана зависимость формы распределения Гаусса от среднеквадратичного отклонения.
Белый шум
[править]Помеху, представляющую собой случайный процесс с равномерным спектром, то есть
называют белым шумом. Мощность белого шума в полосе равна
По-другому, белый шум (рисунок 2) можно определить как стационарный случайный процесс с постоянной спектральной плотностью , равной дисперсии значений — все спектральные составляющие белого шума имеют одинаковую энергию (отсюда аналогия с белым цветом, который содержит все цвета видимого спектра).
Как уже было сказано выше, по своему физическому смыслу спектральная плотность — это мощность процесса, которая приходится на 1 Гц полосы частот. Но тогда идеального белого шума на практике не может существовать, так как для него должно было бы выполняться условие:
где — дельта-функция Дирака. Таким образом, мощность белого шума равна бесконечности, а значения шума не коррелированны для любых , так как корреляционная функция представляет собой дельта-импульс. Тем не менее, многие помехи в радиотехнике, в технике связи и в других отраслях рассматривают как белый шум, если выполняется следующее соотношение между шириной спектров полезных сигналов и шумов
и спектральная плотность шумов слабо изменяется в интервале спектра сигнала.

Примером белого шума может служить тепловой шум. Согласно формуле Найквиста мощность теплового шума, приходящаяся на полосу длиною , равна:
где — постоянная Больцмана, — абсолютная температура. Таким образом, .
Периодический случайный шум
[править]Периодический случайный шум представляет собой результат суммирования синусоид с одинаковыми амплитудами и случайными фазами. Шум содержит все частоты, которые могут быть представлены целым числом периодов на определённом числе выборок.
Распределение периодического шума при большом количестве выборок стремится к гауссову шуму.
Часто периодический шум рассматривают как выборку гауссова шума, ограниченную по величине следующими значениями:
где — заданная амплитуда спектра;
— выборка.

Таким образом, периодический случайный шум имеет импульсный характер, а следовательно дискретную частотную характеристику (рисунок 3).
Способы проникновения шумов
[править]Типичные пути проникновения шумов
[править]Из рисунка 4 видно, что проблема шумоподавления возникает при наличии трёх необходимых элементов: во-первых, должен быть источник шумов; во-вторых, должна быть схема-приёмник, чувствительная к шумам; в-третьих, необходимо наличие канала связи для передачи шумов от источника к приемнику.

При анализе проблемы шумов, прежде всего, следует определить, что является источником шумов, что служит их приёмником и каким образом источник и приёмник связаны друг с другом. Отсюда вытекает, что возможны три способа устранения прохождения шумов:
- подавление шумов в источнике;
- создание приёмника, нечувствительного к шумам;
- минимизация передачи шумов через канал связи.
В некоторых случаях необходимо применять два или даже все три указанных способа подавления шумов.
Шумы, наводимые на провода
[править]Одним из наиболее очевидных, но часто упускаемых из виду путей проникновения шумов в схему являются провода. Проходя через «зашумлённое» пространство, проводник получает шумовые наводки, а затем передаёт их другой схеме. Это вызывает помехи. Решение состоит в защите проводника от шумов или в обеспечении развязки, благодаря которой шумы отводятся с проводника прежде, чем попадут в чувствительную схему.
Основным примером такого вида связи являются шумы, проникающие в схему по проводам сети. В случае, если разработчик не имеет возможности контролировать сеть или если к сети подключают и другую аппаратуру, возникает необходимость в развязке проводов сети по шумам до их подсоединения к схеме.
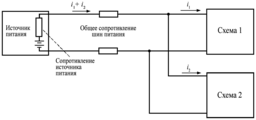
Связь через общее сопротивление
[править]Связь через общее сопротивление встречается там, где токи от двух различных схем проходят через одно сопротивление. При этом падение напряжения, создаваемое каждой из схем на этом сопротивлении, является для другой схемы помехой. Классический пример такого рода связи показан на рисунке 5, а. Оба возвратных тока (1 и 2) проходят на землю через общее сопротивление. Что касается схемы 1, то потенциал ее общей точки относительно земли модулируется возвратным током 2, протекающим через общее сопротивление шины земли. Поэтому от схемы 2 к схеме 1 через общее сопротивление поступает некоторый шумовой сигнал.
-
а)
-
б)
Другим примером проблемы такого рода является представленная на рисунке 5, б схема разводки питания. Любое изменение тока, потребляемого схемой 2, будет изменять напряжение на зажимах питания схемы 1 из-за наличия общих сопротивлений шин питания и внутреннего сопротивления источника питания. Положение можно несколько улучшить, подключив схему 2 ближе к выходным зажимам источника питания и уменьшив тем самым величину общего сопротивления шин питания. Однако связь через внутреннее сопротивление источника питания остаётся.
Электрические и магнитные поля
[править]Еще один вид связи представляет собой излучение электрического и магнитного полей. Все элементы схем, включая проводники, при движении по ним электрических зарядов излучают электромагнитные поля. Кроме такого не предусмотренного разработкой излучения, существует проблема преднамеренного излучения от таких источников, как радиовещательные и радиолокационные станции. Когда приёмник расположен вблизи источника (в ближнем поле), электрическое и магнитное поля рассматривают раздельно. Если же приемник находится далеко от источника (в дальнем поле), излучение рассматривается как комбинация электрического и магнитного полей, то есть как электромагнитное излучение.

Это имеет место, например, в схеме, показанной на рисунке 6. В этой схеме экранированный двигатель постоянного тока соединен со схемой управления. Шумы от двигателя вызывают помехи в слаботочной схеме, расположенной в той же установке. Шумовые токи, возникающие на коллекторе двигателя, выходят за пределы экрана, проходя по проводам к схеме управления. Провода излучают шумы, наводя их на слаботочные цепи.
В этом примере источником шумов является искрение между щетками и коллектором двигателя. Канал связи состоит из двух частей: проводов, подведённых к двигателю, и излучения от этих проводов. Приёмником служит слаботочная цепь. В данном случае шумы источника и приёмника практически не устранимы. Поэтому помехи должны быть подавлены в канале связи. Можно блокировать шумы, проходящие по проводам за пределы экрана, или подавить излучение проводов.
Второстепенные источники шумов
[править]Гальванический процесс. При использовании в слаботочной сигнальной цепи разнородных металлов в результате образования из них гальванической пары могут возникать напряжения шумов. При наличии на стыке двух металлов загрязнений или водяных паров создается электрохимический элемент. Развиваемая им ЭДС зависит от используемых металлов, то есть от их расположения в, так называемом, гальваническом ряду. Чем дальше в этом ряду металлы отстоят друг от друга, тем больше будет развиваемое ими напряжение. Если контакт образован одноимёнными металлами, разность потенциалов между ними отсутствует.
При использовании разнородных металлов, помимо возникновения напряжения шумов, может существовать и проблема коррозии. Гальваническая коррозия приводит к тому, что положительные ионы одного металла переносятся в другой металл. Это постепенно разрушает материал анода. Скорость коррозии зависит от степени загрязнения окружающей среды и от того, насколько далеко отстоят друг от друга металлы в гальваническом ряду. Чем дальше они расположены в этом ряду, тем быстрее происходит перенос ионов. Самой распространённой комбинацией металлов является медь и алюминий. При этом алюминий в конце концов разъедается. Однако, если медь покрыта оловянно-свинцовым припоем, реакция замедляется, поскольку медь и оловянно-свинцовый припой расположены в гальваническом ряду ближе, чем медь и алюминий.
Для гальванического процесса необходимо наличие четырёх элементов:
- материала анода;
- электролита (здесь — в виде загрязнения);
- материала катода;
- электропроводного соединения между анодом и катодом (обычно представляет собой цепь утечки).
Гальванический процесс может иметь место даже в том случае, если между анодом и катодом нет загрязнения. Всё, что необходимо для возникновения гальванического процесса, это некоторое количество грязи на поверхности соприкосновения двух металлов.
Электролитический процесс. Другой вид коррозии обусловлен электролитическим процессом. Он вызывается постоянным током, протекающим между двумя металлами при наличии между ними электролита (в качестве последнего может фигурировать грязь даже со слабыми кислотными свойствами). Коррозия такого типа не зависит от вида применяемых металлов и наблюдается даже между однородными металлами. Скорость коррозии зависит от величины тока и проводимости электролита.
Трибоэлектрический эффект. В том случае, если диэлектрик внутри кабеля не имеет контакта с проводниками кабеля, на нём может накапливаться заряд. Это явление называется трибоэлектрическим эффектом. Обычно он вызывается механическим изгибом кабеля. Такой заряд действует как источник напряжения шумов, находящийся внутри кабеля. Трибоэлектрический эффект минимизируют, избегая резких перегибов кабеля и его перемещения. Выпускается специальный «малошумящий» кабель, в котором диэлектрик проходит специальную химическую обработку, сводящую к минимуму возможность накопления на нём заряда.
Перемещение проводника. Если проводник движется в магнитном поле, на концах его возникает разность потенциалов. Паразитные магнитные поля, вызванные наличием больших токов в силовых цепях, а также в других схемах, имеются почти в любой точке окружающего пространства. Данная проблема усугубляется при наличии вибрации. Решается она устранением перемещения проводников путём закрепления кабелей скобами и другими приспособлениями.
Индустриальные помехи
[править]Вопросу изучения явлений, порождающих индустриальные помехи, и методов предотвращения их возникновения в последнее время уделяется значительное внимание. Проведенные исследования показали, что как плотности, так и спектральный состав помех промышленного происхождения существенно отличаются в различных, подчас близко расположенных друг к другу районах. Наиболее высокие плотности этих помех наблюдаются в больших городах и прилегающих к ним местностях.
Источники помех здесь можно разделить на две большие группы. К первой группе относятся устройства, генерирующие относительно регулярные высокочастотные колебания, не предназначенные для излучения, такие, как системы развертки электронно-лучевых трубок, различного рода промышленные, медицинские высокочастотные установки и так далее. Помехи, излучаемые такими источниками, как на основной рабочей частоте, так и на гармониках представляют собой колебания, близкие к синусоидальным. Эти источники относительно легко определяются, допускают простое прогнозирование эффектов, порождаемых их воздействием, но нелегко контролируются.
К источникам второй группы, являющейся наиболее обширной, относятся различные электрические устройства, не вырабатывающие периодических высокочастотных сигналов. К ним относятся линии передачи электроэнергии, системы зажигания автомобильных двигателей, высокочастотная аппаратура для дуговой сварки, газоразрядные устройства, динамомашины, генераторы электрического тока, индукционная и переключающая аппаратура.
Исследования показали, что «удельные веса» той или иной группы источников помех оказываются приблизительно одинаковыми в различных районах с примерно одинаковым уровнем развития промышленности. Так, в крупных промышленных центрах и прилегающих к ним районах основными источниками помех рассматриваемого типа являются системы зажигания двигателей внутреннего сгорания, линии электропередачи и аппаратура, используемая при дуговой сварке.
На частотах, превышающих 30 МГц, помехи, порождаемые системами зажигания, обычно преобладают над помехами, создаваемыми другими источниками. На частотах же, меньших 30 МГц, преобладающими обычно являются помехи, порождаемые линиями электропередачи.
Помехи от системы зажигания автомобильного двигателя представляют собой приблизительно периодический импульсный сигнал сложной формы. При скоплении в различных точках большого числа автомобилей, движущихся с различными скоростями, измеряющая аппаратура регистрирует серии импульсов со случайными амплитудами и временны́ми интервалами. Длительность регистрируемых групп импульсов колеблется в пределах от нескольких микросекунд до нескольких миллисекунд, а длительность отдельных импульсов от 1 до 6 нс.
В современном городе общая интенсивность помех рассматриваемого типа характеризуется суточными изменениями приблизительно в 16 дБ (между периодами максимальной и минимальной плотности движения). При этом наблюдается корреляция абсолютного уровня помех с численностью населения в городе. Рассматриваемый вид индустриальных помех практически всегда преобладает над другими их типами в полосах местности шириной 60—80 м, прилегающих к автострадам и шоссе с интенсивным автомобильным движением.
Помехи от линий электропередач. Высоковольтная аппаратура и линии передачи электроэнергии создают помехи, которые достигают максимальной интенсивности во время дождя, снега, тумана и высокой относительной влажности воздуха.
В засушливых районах увеличению интенсивности помех способствует большая турбулентность воздуха и повышенный уровень солнечной радиации. Уровень помех резко возрастает при неисправности линии передачи.
Помехи от высоковольтных линий передачи носят случайный характер и имеют форму непрямоугольных импульсов, длительность которых существенно превосходит ширину помеховых импульсов, вызываемых работой систем зажигания автомобильных двигателей. Частоты же следования помеховых импульсов от линий электропередач значительно ниже частот следования помеховых импульсов от систем зажигания.
Причиной возникновения помех от линий электропередачи являются переходные процессы, вызываемые электрическими разрядами, которые хаотически возникают на поверхностях проводников и изоляторов линии. Импульсные токи, появляющиеся при таких разрядах, распространяются вдоль линии, которая может выступать либо в качестве коаксиального волновода (в этом случае поток энергии ограничивается внутренним проводом и оплеткой), либо в качестве одиночной линии над земной поверхностью.
Помехи от аппаратуры дуговой сварки. Аппаратура дуговой сварки создает помехи очень высокого уровня. Только тот факт, что в пределах каждого локального района одновременно может работать, как правило, лишь незначительное количество таких аппаратов, не делает эту аппаратуру основным источником индустриальных помех. Чего нельзя сказать о машиностроительных предприятиях с интенсивным использованием сварочной техники. Спектры помех, возникающих при работе аппаратуры различной конструкции, не совпадают друг с другом. Результаты измерений, проведенных с большим числом аппаратов разной конструкции, показали наличие трёх широких резонансных полос, центры которых соответствуют частотам 750 кГц, 3 МГц и 20 МГц. Спектр излучения каждого отдельно взятого аппарата не обязательно включает в себя все три резонансные полосы.
Технические методы устранения помех
[править]В своей работе «Методы подавления шумов и помех в электронных системах»[2] Г. Отт перечислил основные методы и дал практические рекомендации по борьбе с помехами:
- экранирование;
- заземление;
- балансировка;
- фильтрация;
- изоляция;
- разнесение и ориентация;
- регулировка величины полного сопротивления схемы;
- выбор кабеля;
- подавление (в частотной или временной области).
Подавление шумов в источнике
[править]- Необходимо заключать источники шумов в экран.
- Необходимо подключать фильтры ко всем проводникам, проходящим в зашумленном пространстве.
- Необходимо ограничивать время нарастания импульса.
- Для катушек реле следует предусмотреть цепи подавления выбросов напряжения.
- Необходимо скручивать шумящие проводники.
- Необходимо экранировать витые пары шумящих проводов.
- Необходимо заземлять оба конца экранов, используемых для подавления помех излучения (экраны не обязательно должны быть изолированы).
Устранение связи по шумам
[править]- Необходимо скручивать проводники с малым уровнем сигнала.
- Необходимо располагать малосигнальные проводники ближе к шине (особенно при высоком уровне полного сопротивления цепи).
- Необходимо скручивать и экранировать сигнальные проводники (на высоких частотах можно использовать коаксиальный кабель).
- В экранированных кабелях, используемых для защиты малосигнальных проводов, экраны следует заземлять только с одного конца (на высоких частотах можно применять коаксиальный кабель с экраном, заземленным с обоих концов).
- Необходимо изолировать экран сигнальных проводов от случайного заземления в непредусмотренной точке.
- Когда малосигнальные и шумящие провода проходят через общий разъём, необходимо их разделять, помещая между ними заземлённые провода.
- Необходимо пропускать экранирующую оплётку сигнальных проводов через отдельный контакт разъёма.
- Необходимо избегать использования общих проводов заземления для устройств с высоким и низким уровнями сигнала.
- Необходимо выполнять заземление оборудования так, чтобы оно было отделено от земель схем.
- Необходимо выполнять заземление возможно более короткими проводами.
- Для защиты металлических поверхностей необходимо применять проводящие покрытия.
- Необходимо разносить шумящие и не создающие шумов проводники.
- Необходимо заземлять цепи только в одной точке (кроме высокочастотных цепей).
- Необходимо избегать ненадёжных или случайных заземлений.
- Для очень чувствительных схем необходимо использовать источник и нагрузку, симметричные относительно земли.
- Необходимо заключать чувствительные устройства в экранирующие корпуса.
- Необходимо ставить фильтры или цепи развязки на любой проводник, входящий в корпус с заключённым в нем чувствительным устройством.
- Необходимо делать чувствительные проводники как можно короче.
- Необходимо делать как можно короче проводники, выходящие за пределы экрана кабеля.
- Необходимо применять для разводки питания шины с малым полным сопротивлением.
- Необходимо избегать образования контуров заземления.
- Необходимо внимательно рассмотреть использование для разрыва контуров заземления следующих устройств:
- изолирующих трансформаторов;
- нейтрализующих трансформаторов;
- оптронов;
- дифференциальных усилителей;
- усилителей с защитным экранированием;
- балансных схем.
Подавление шумов в приёмнике
[править]- Не следует делать полосу пропускания шире, чем это необходимо.
- По возможности необходимо использовать селективные частотные фильтры.
- Необходимо обеспечивать соответствующую развязку по питанию.
- Необходимо шунтировать электролитические конденсаторы с малой ёмкостью, работающие на высокой частоте.
- Необходимо разделять сигнальные, шумящие и корпусные земли.
- Необходимо применять экранирующие корпуса.
- У трубчатых конденсаторов необходимо заземлять внешнюю обкладку.
Методы защиты от помех офисных и промышленных сетей
[править]Различают локальные вычислительные сети (ЛВС) для офисного (домашнего) и промышленного применения. В офисных приложениях ЛВС к ним предъявляются в основном требования по скорости передачи данных (особенно это актуально для мультимедиа-приложений реального времени). В офисных и домашних условиях уровень помех не так сильно велик, по сравнению с производственными, поэтому в правильно сконфигурированных сетях коллизии возникают редко. Минимальные простои, связанные с повторной передачей искаженных и потерянных пакетов данных, не так критичны, как в промышленных сетях. В приложениях интернет-вещания в режиме реального времени неправильные кадры могут быть восстановлены по экстраполяционному принципу, основываясь на предыдущих данных, так как обычно искажения такого рода малозаметны или имеют приемлемый характер.
К сетям полевого уровня (fieldbus), напротив, предъявляются жесткие требования по помехоустойчивости и предсказуемости. Обычно к промышленным сетям предъявляются следующие требования:
- жёсткая детерминированность поведения;
- обеспечение функций реального времени;
- работа на длинных линиях с использованием недорогих физических сред (в частности, витой пары);
- повышенная надёжность физического и канального уровней передачи данных в условиях производственной среды (например, при наличие мощных электромагнитных помех);
- наличие специальных высоконадежных механических соединений компонентов, обеспечивающих защиту контактов от агрессивной производственной среды.
В настоящий момент в промышленности пользуется популярностью расширение «офисного» Ethernet (IEEE 802.3) — Industrial Ethernet.
Стандарт Industrial Ethernet определяет проводные соединения и электрические сигналы на физическом уровне, формат пакетов и протоколы управления доступом к среде. В Industrial Ethernet применяются промышленные витые пары (англ. Industrial Twisted Pair, ITP) с двойным экранированием, IE FC TP-кабелей для быстрого монтажа и ТР-кордов или стеклянные оптоволоконные кабели.
Дополнение стека протоколов TCP/IP протоколом RFC 1006 обеспечивает регулярную и частую передачу по сети небольших объемов информации, что свойственно для обмена данными между промышленными контроллерами.
C помощью специальных коммутаторов можно организовать кольцевую топологию, которая при обрыве восстанавливает связь, то есть находит новый путь для передачи данных значительно быстрее, чем применяемый в обычных сетях «алгоритм избыточного дерева». При этом используется алгоритм резервирования, который позволяет провести реконфигурацию сети за 0,3 с.
Метод управления доступом — множественный доступ с контролем несущей и обнаружением коллизий (англ. Carrier Sense Multiple Access with Collision Detection, CSMA/CD). Скорость передачи данных для Industrial Ethernet составляет 10 Мбит/с, а для Industrial Fast Ethernet (IEEE 802.3u) — 100 Мбит/с, размер пакета данных — от 72 до 1526 байт.
Для защиты от помех в офисных и промышленных ЛВС применяют следующие методы:
- Применение витой пары в качестве среды передачи данных. Витые пары с двойным экранированием позволяют подавить синфазную помеху на 70 дБ.[3]
- Применение волоконно-оптических кабелей в качестве среды передачи данных, которые менее подвержены электромагнитным помехам. Но с другой стороны, этот метод сопряжен с накладными расходами по приобретению дополнительных модулей сопряжения с оптическими устройствами.[3]
- Применение кодирования (см. ниже):
- В сетях классического Ethernet для передачи данных используется импульсная модуляция на основе манчестерского кодирования. Это импульсный код с самосинхронизацией: логическая единица кодируется перепадом потенциала от низкого уровня сигнала к высокому, а логический ноль — наоборот. Уровень высокого сигнала составляет плюс 0,85 В, низкого — минус 0,85 В. В Fast Ethernet и Gigabit Ethernet применяется избыточное кодирование: 4B/5B для первого и 8B/10B — для второго.[4]
- На уровне физического кодирования в сетях TokenRing (IEEE 802.5) применяется дифференциальное манчестерское кодирование.[5]
- В промышленной сети PROFIBUS (англ. PROcess FIeld BUS), описанной в EN 50170, используется способ передачи RS-485, базирующийся на полудуплексной, асинхронной синхронизации. Для физического кодирования используется код без возврата к нулю (англ. Non-Return to Zero, NRZ).
- В сетях CAN (англ. Controller Area Network, ISO 11898) также применяется NRZ-кодирование.
- В ЛВС для связи устройств АСУТП Foundation Fieldbus (IEC 61158-2) сигналы полевой шины шифруются кодом Манчестер biphase-L (англ. Manchester bi-φ-L).
- В некоторых случаях при передаче данных на физическом уровне OSI применяется скремблирование. Скремблирование — это приведение информации к виду, по различным характеристикам похожему на случайные данные, что выравнивает спектр сигнала, частоты появления различных символов и их цепочек, а это позволяет подавить слишком сильные спектральные составляющие сигнала, которые вызывают нежелательные наводки на соседние линии и излучение в окружающую среду.
- Для достоверности принятой информации на канальном уровне применяют дополнение пакета данных некой служебной информацией о целостности пакета. Это может быть простая контрольная сумма, выраженная в виде бита чётности (см. ниже) или же набор битов. Наиболее распространенным методом верификации принятых данных является избыточный циклический контроль CRC (англ. Cycled Redundancy Control), и в частности, его 16-битная реализация — CRC16.
- Для увеличения надёжности применяют резервирование линий передачи данных. Например, в сетях TokenRing используется топология типа «кольцо», которая имеет преимущество по сравнению с другими типами топологий в том, что при обрыве одной связывающей линии данные будут передаваться через другую. Протокол Ethernet не позволяет использовать данный способ напрямую, но контроллеры сети Industrial Ethernet имеют возможность использовать некоторые свои входы/выходы для целей резервирования и включать их в работу во время обрыва основной линии.
- Переход в АСУТП на полевом уровне от аналогового сигнала (чаще всего, 4—20 мА) к цифровому позволяет повысить достоверность показаний измерительных приборов, так как в цифровой сигнал имеет конечное количество состояний.
- Имеется возможность совместного использования аналоговых и цифровых сигналов. Такую возможность предоставляет протокол первичной связи HART (англ. Highway Addressable Remote Transducer — адресуемый дистанционный магистральный преобразователь). Данный протокол основан на методе передачи данных с помощью частотной модуляции (англ. Frequency Shift Keying, FSK, ЧМ) в соответствие со стандартом Bell 202. Цифровая информация передаётся частотами 1200 Гц (логическая единица) и 2200 Гц (логический ноль), которые накладываются на аналоговый токовый сигнал. Так как частотно-модулированный сигнал является двуполярным, то при применении однополосной низкочастотной фильтрации аналоговые приборы не будут чувствительны к цифровому сигналу (фильтр с полосой пропускания 10 Гц вносит искажение в исходный сигнал в ±0,01 % от максимального значения аналогового сигнала).[3]
Устранение помех канальным кодированием
[править]Под кодированием понимается процесс представления определённых данных с помощью ограниченного набора представлений — символов. Кодовые комбинации образовываются по некой наперёд заданной совокупности правил кодирования. Данная совокупность образует так называемую систему кодирования. Обратное преобразование информации называется декодированием.
При передаче данных используется так называемое канальное кодирование, которое представляет собой класс преобразований сигнала, выполняемых для повышения качества связи. В результате этого сигнал становится менее уязвимым к шуму, помехам и замираниям. Данный метод позволил более чем на 10 дБ повысить производительность при значительно меньших затратах по сравнению с другими методами, например методами увеличения мощности передатчика или размера антенны.
Кодирование сигнала и структурированные последовательности
[править]Тему канального кодирования можно условно разделить на два раздела: кодирование (или обработка) сигнала и структурированные последовательности (или структурированная избыточность). Кодирование сигнала означает преобразование сигнала в некий «улучшенный сигнал», позволяющий сделать процесс детектирования менее подверженным ошибкам. Метод структурированных последовательностей — это преобразование последовательности данных в новую, «улучшенную последовательность», обладающую структурной избыточностью (которая вмещает избыточные биты). Эти избыточные разряды служат для определения и исправления ошибок. На выходе процедуры кодирования получается закодированный (формой сигнала или структурированной последовательностью) сигнал, имеющий лучшие пространственные характеристики, чем некодированный.
Для оценки целесообразности применения кодирования вводится понятие эффективности кодирования. При данной вероятности битовой ошибки эффективность кодирования определяется как уменьшение нормированного отношения «сигнал/шум» , которое достигается при использовании кодирования. Эффективность кодирования выражается в децибелах:
где и — значения для исходного и кодированного сигнала соответственно.
Нормированное отношение «сигнал/шум» определяется как
где — энергия бита;
— спектральная плотность мощности шума;
— время передачи одного бита;
— скорость передачи битов;
— ширина полосы.
Кодирование сигнала
[править]Для кодирования информации используют различные сигналы. Рассмотрим некоторые из них.

Антиподные сигналы являются зеркальными отображениями друг друга, либо один сигнал является отрицательным по отношению к другому, либо они различаются между собой на 180° (противофазные сигналы). На рисунке 7 изображён набора синусоидальных антиподных сигналов таких, что , .
Набор равноэнергетических сигналов , , называется ортонормированным (ортогональным), если выполняется условие:
где — коэффициент взаимной корреляции;
— символ Кронекера;
— энергия сигнала
Примером таких сигналов могут служить гармонические функции. На рисунке 8 изображены сигнал и , .

Ортогональными могут быть также наборы импульсных сигналов. На рисунке 9 показан набор ортогональных сигналов, которые имеют вид импульсов, имеющих следующее аналитическое выражение: и , . Импульс имеет длительность , где — период.

Если расширить значение коэффициента взаимной корреляции в область отрицательных значений, то антиподные сигналы можно считать частным случаем ортогональных сигналов с .
Временно́е разделение сигналов позволяет осуществлять -арную передачу сигналов, при которой процессор за один такт работы принимает бит данных. Процессор указывает модулятору произвести один из сигналов. Частным случаем при является двоичная передача сигнала. При -арную передачу сигналов можно рассматривать как процедуру кодирования формы сигнала. При ортогональной передаче сигналов увеличение приводит к повышению достоверности передачи или уменьшению требуемого за счёт увеличения полосы пропускания. При неортогональной передаче сигналов улучшение эффективности использования полосы пропускания происходит за счёт снижения достоверности передачи или возрастания требуемого .
Как уже было сказано выше, процедура кодирования сигнала состоит в преобразовании набора сигналов (представляющих набор сообщений) в усовершенствованный набор сигналов, но при этом каждый сигнал набора пытаются сделать настолько непохожим на другие, насколько это возможно. Это требование выражает значение коэффициент взаимной корреляции , которое должно быть как можно меньше. Строго это условие выполняется тогда, когда сигналы антикоррелируют (при ). Этого можно добиться только в том случае, если в наборе всего два значения () и они антиподны друг другу. На практике используют набор сигналов с большим количеством элементов. Поэтому наименьшее значение , что соответствует системе ортогональных сигналов.
Ортогональные коды
[править]Для набора кодовых слов, состоящего из сигналов, условие ортогональности примет вид:
где — количество совпавших бит;
— количество несовпавших бит;
— общее количество бит в последовательности.
Набор однобитовых данных можно преобразовать с помощью ортогональных кодовых слов, состоящих из двух разрядов каждое, которые описываются строками матрицы :
| Набор данных | Набор ортогональных кодовых слов | |
Вообще, для набора -битовых данных из матрицы можно построить набор кодовых слов размерностью , который называется матрицей Адамара:
где черта над означает логическое отрицание.
Каждая пара слов в каждом наборе кодовых слов содержит одинаковое количество совпадающих и несовпадающих разрядов, поэтому, в соответствии с уравнением (28), (при ) и каждый из этих наборов ортогонален.
Для одинаковых, равноэнергетических ортогональных сигналов вероятность ошибки в кодовом слове (символе) , можно оценить сверху, как
где — размер набора кодовых слов;
— число информационных бит;
— энергия кодового слова;
— энергия одного бита;
— спектральная плотность мощности шума;
— гауссов интеграл ошибки, равный:
Вероятность появления ошибочного бита можно определить как:
Модификацией ортогонального кода является биортогональный код. Биортогональный набор сигналов, состоящий из кодовых слов (сигналов), получается из ортогонального набора, состоящего из сигналов, путем дополнения последнего отрицанием каждого сигнала:
Биортогональный набор состоит из комбинации ортогональных и антиподных сигналов, поэтому если использовать коэффициент , то биортогональные коды можно представить следующим образом:
Одно из преимуществ биортогональных кодов перед ортогональными заключается в том, что при передаче аналогичной информации размер кодового слова биортогональных кодов вдвое меньше размера кодового слова ортогональных кодов. Следовательно, при использовании биортогональных кодов требования к полосе пропускания вдвое слабее, чем при использовании ортогональных кодов. Поскольку антиподные векторы сигналов имеют лучшие пространственные характеристики, чем ортогональные.
Для одинаковых, равноэнергетических биортогональных сигналов вероятность ошибки в кодовом слове (символе) можно оценить следующим образом:
Для биортогональных кодов довольно трудно получить оценку , поэтому пользуются следующей аппроксимацией, имеющей место при , или :
Описанные биортогональные коды значительно снижают по сравнению с ортогональными кодами и требуют только половину полосы пропускания ортогональных кодов.
Код, получаемый из ортогонального ряда путём удаления первого разряда каждого кодового слова, называется трансортогональным, или симплексным кодом. Такой код описывается следующими значениями :
С точки зрения минимальной энергии, необходимой для поддержания заданной вероятности ошибки, симплексный код эквивалентен равновероятному ортогональному набору.
Сравнивая достоверность передачи ортогонального, биортогонального и симплексного кодов, можно сказать, что симплексный код имеет наименьшее требуемое для получения определенной частоты появления символьных ошибок. Впрочем, при больших все три схемы очень похожи между собой в смысле достоверности передачи. При этом биортогональное кодирование, по сравнению с другими методами, требует лишь половины полосы пропускания.
Структурированные последовательности
[править]Структурированные последовательности делятся на три подкатегории:
- блочные;
- свёрточные;
- турбокоды.
Рассмотрим каждый из этих типов.
При использовании блочных кодов исходные данные делятся на блоки из бит, которые называют информационными битами, или битами сообщения. Каждый блок может представлять любое из отдельных сообщений. В процессе кодирования каждый -битовый блок данных преобразуется в больший блок из бит, который называется кодовым битом, или канальным символом. К каждому блоку данных кодирующее устройство прибавляет бит, которые называются избыточными битами, или контрольными битами. Если , то контрольный бит называется битом чётности, или битом паритета (от англ. parity — чётный). Новой информации контрольные биты не несут. Блочные коды обозначаются как .
Отношение числа избыточных бит к числу информационных бит:
называется избыточностью кода.
Отношение числа бит данных к общему числу бит носит название степень кодирования. Под степенью кодирования подразумевается доля кода, которая приходится на полезную информацию. Например, в коде со степенью 1/2, каждый кодовый бит несёт 1/2 бита информации.
Коды с контролем чётности для обнаружения или исправления ошибок используют линейную сумму информационных битов, которая представляется одним контрольным битом, который позже прибавляется к блоку информационных битов. Этот бит (бит чётности) может быть равен нулю или единице, причём его значение выбирается так, чтобы сумма всех битов в кодовом слове была чётной или нечётной. В операции суммирования используется арифметика по модулю 2 (операция исключающего ИЛИ). Если бит чётности выбран так, что результат чётный, то говорят, что схема имеет положительную чётность; в противном случае, говорят об отрицательной чётности.
Расширением кодов с битом паритета является прямоугольный, или композиционный код. Он создаётся следующим образом. Вначале из битов сообщения строится прямоугольник, состоящий из строк и столбцов. Затем к каждой строке и каждому столбцу прибавляется бит чётности, что в результате даёт матрицу размером . Любая отдельная ошибка в разряде приведёт к нарушению чётности в одном столбце и в одной из строк матрицы. Следовательно, прямоугольный код может исправить любую единичную ошибку, поскольку расположение такой ошибки однозначно определяется пересечением строки и столбца, в которых была нарушена чётность.
Линейные блочные коды — это класс кодов с контролем чётности, которые можно описать парой чисел . В процессе кодирования блок из символов сообщения (вектор сообщения) преобразуется в больший блок из символов кодового слова (кодовый вектор), образованного с использованием элементов данного алфавита. Если алфавит состоит только из двух элементов (0 и 1), код является двоичным и включает двоичные разряды (биты). Это самые распространённые виды линейных блочных кодов.
-Битовые сообщения формируют набор из последовательностей сообщения, называемых -кортежами (последовательностями цифр). Процедура кодирования сопоставляет с каждым из -кортежей сообщения один из -кортежей. Следовательно, линейные блочные коды представляют взаимно однозначное соответствие, которое производится согласно, так называемой, таблице соответствия. Данный вид кодов используется в расширении сетевой технологии Ethernet: в Fast Ethernet используется код 4B/5B — кодирование 4 битов информации 5 канальными битами, в Gigabit Ethernet — 8B/10B (8 бит информации — 10 канальных бит).
Важным подклассом линейных блочных кодов являются двоичные циклические коды. Линейный код называется циклическим, если он обладает следующим свойством. Если -кортеж является кодовым словом, тогда -кортеж , полученный из с помощью циклического сдвига, также является кодовым словом. Вообще, , полученный циклическими сдвигами, является также является кодовым словом. Данный код легко реализуется на регистре сдвига с обратной связью.
Коды Хэмминга — это простой класс блочных кодов, которые имеют следующую структуру:
где Они способны исправлять все однобитовые ошибки или определять все модели из двух ошибок в блоке. Для декодирование кодов Хэмминга особенно хорошо подходят, так называемые, синдромы — матрицы, представляющие собой результат проверки чётности, выполняемой над сигналом для определения его принадлежности заданному набору кодовых слов. Хотя коды Хэмминга не являются слишком мощными, они принадлежат к очень ограниченному классу блочных кодов, называемых совершенными.
Одним из наиболее практичных блочных кодов является двоичный расширенный код Голея , который образован путём прибавления битов чётности к совершенному коду , известному как код Голея. Эти дополнительные биты дают степень кодирования 1/2, реализовать которую проще (с точки зрения системного тактового генератора), чем степень кодирования кода Голея, равную 12/23. Расширенный код Голея значительно мощнее рассмотренного выше кода Хэмминга. Цена, которую приходится платить за повышение эффективности, заключается в более сложном декодере и, соответственно, более широкой полосе пропускания.
Коды Боуза — Чоудхури — Хоквенгема (БЧХ-коды) являются результатом обобщения кодов Хэмминга, которое позволяет исправлять множественные ошибки. Они составляют мощный класс циклических кодов, который обеспечивает достаточную свободу выбора длины блока, степени кодирования, размеров алфавита и возможностей коррекции ошибок. Коды БХЧ очень важны, поскольку при блоках, длина которых равна порядка несколько сотен, коды БХЧ превосходят своими качествами все другие блочные коды с той же длиной блока и степенью кодирования. В наиболее часто применяемых кодах БХЧ используется двоичный алфавит и блок кодового слова длиной , где
Коды Рида — Соломона — это недвоичные циклические коды, символы которых представляют собой -битовые последовательности, где . Коды Рида — Соломона определены на -битовых символах при всех и , для которых , где — число информационных битов, подлежащих кодированию, а — число кодовых символов в кодируемом блоке. Для большинства кодов Рида — Соломона
где — количество ошибочных битов в символе, которые может исправить код, а — число контрольных символов. Расширенный код Рида — Соломона можно получить при или , но не более того.
Коды Рида — Соломона чрезвычайно эффективны для исправления пакетов ошибок, поэтому их разновидность, называемая кодом Рида — Соломона с перекрестным чередованием (англ. cross-interleave Reed — Solomon code, CIRC), используется в системе цифровой записи на компакт-дисках (англ. compact disc digital audio, CD-DA). В данном случае существует несколько источников канальных ошибок: маленькие нежелательные частички или воздушные пузырьки в материале пластика или неточное расположение впадин при изготовлении диска и отпечатки пальцев или царапины, появившиеся при эксплуатации. Можно сказать, что канал, в основном, склонен вносить пакетоподобные ошибки, поскольку царапины или пятна от пальцев будут вызывать ошибки в нескольких последовательных фрагментах данных.
Рассмотрим теперь свёрточные коды. Для их реализации используются специальные свёрточные кодеры. Рассмотрим принцип их работы.
Исходное сообщение на входе обозначается последовательностью , где — двоичный знак (бит), а — индекс времени. Предполагается, что все равновероятно равны единице или нулю и независимы между собой. Будучи независимой, последовательность битов нуждается в некоторой избыточности, то есть знание о бите не даёт никакой информации о бите (при ). Кодер преобразует каждую последовательность в уникальную последовательность кодовых слов . Даже несмотря на то, что последовательность однозначно определяет последовательность , ключевой особенностью свёрточных кодов является то, что данный -кортеж внутри не однозначно определяет связанные с ним -кортежи внутри , поскольку кодирование каждого из -кортежей является функцией не только -кортежей, но и предыдущих -кортежей. Последовательность можно разделить на последовательность кодовых слов: Каждое кодовое слово состоит из двоичных кодовых символов, часто называемых канальными символами, канальными битами, или битами кода, в отличие от битов входного сообщения, кодовые символы не являются независимыми.

Обычный свёрточный кодер, показанный на рисунке 10, реализуется -разрядным регистром сдвига и сумматорами по модулю 2, где — длина кодового ограничения. Длина кодового ограничения — это количество -битовых сдвигов, после которых один информационный бит может повлиять на выходной сигнал кодера. В каждый момент времени на место первых разрядов регистра перемещаются новых бит. Все биты в регистре смещаются на разрядов вправо, и выходные данные сумматоров последовательно дискретизируются, давая, в результате, биты кода. Затем эти символы кода используются модулятором для формирования сигналов, которые будут переданы по каналу. Поскольку для каждой входной группы из бит сообщения имеется бит кода, степень кодирования равна бит сообщения на бит кода, где .
Наиболее часто используются двоичные свёрточные кодеры, для которых , то есть биты сообщения сдвигаются по одному биту за такт. Таким образом, за -й момент времени бит сообщения будет перемещён на место первого разряда регистра сдвига, все предыдущие биты в регистре будут смещены на один разряд вправо, а выходной сигнал сумматоров будет последовательно оцифрован и передан. Поскольку для каждого бита сообщения имеется бит кода, то степень кодирования равна . Имеющиеся в момент времени кодовых символов составляют -е кодовое слово ветви , где () — это -й кодовый символ, принадлежащий -му кодовому слову ветви.
Для описания свёрточного кода нужно определить кодирующую функцию . Для этого существует несколько методов, наиболее наглядный из которых является представление функции в виде древовидной диаграммы, где каждый лист является одной из возможных альтернатив значения .
Для приёма сообщений, представленных свёрточными кодами, используются свёрточные декодеры. При передаче информации по линиям связи в зашумленной среде неизбежно происходит искажение информации. Поэтому цель декодера не просто обратить действие кодера на информацию, но и сделать это с максимально возможной степенью правдоподобия.
Принятие решений о том, что принятая искажённая последовательность соответствует переданной, основывается на принципе максимального правдоподобия. Принцип — это формализация способа принятия решений, основанного на «здравом смысле», когда имеются статистические данные о вероятностях. В основу принципа положено предположение, что если все входные последовательности сообщений равновероятны, то минимальная вероятность ошибки получается при использовании декодера, который сравнивает условные вероятности и выбирает максимальную. Условные вероятности также называются функциями правдоподобия , где — это принятая последовательность, а — одна из возможных переданных последовательностей. Декодер выбирает , если
Улучшением декодера максимального правдоподобия являются декодеры, построенные по алгоритму декодирования Витерби. Данный алгоритм уменьшает вычислительную нагрузка за счёт использования особенностей структуры конкретной решётки кода. Преимущество декодирования Витерби, по сравнению с декодированием по методу «грубой силы», заключается в том, что сложность декодера Витерби не является функцией количества символов в последовательности кодовых слов. Алгоритм включает в себя вычисление расстояния (мера подобия) между сигналом, полученным в момент времени и всеми путями решётки, входящими в каждое состояние в момент времени . В алгоритме Витерби не рассматриваются те пути решётки, которые, согласно принципу максимального правдоподобия, заведомо не могут быть оптимальными. Если в одно и то же состояние входят два пути, выбирается тот, который имеет лучшую метрику; такой путь называется выживающим. Отбор выживающих путей выполняется для каждого состояния. Таким образом, декодер углубляется в решётку, принимая решения путём исключения менее вероятных путей. Предварительный отказ от маловероятных путей упрощает процесс декодирования.
В качестве меры подобия используется расстояние Хэмминга — метрика различия объектов одинаковой размерности. Расстоянием Хэмминга между двумя двоичными последовательностями и длины называется число позиций, в которых они различны.
Турбокоды впервые были введены в 1993 году Берру, Главье и Цитимаджимой. Турбокод можно считать обновлением структуры каскадного кодирования с итеративным алгоритмом декодирования связанной кодовой последовательности. Схема каскадного кодирования впервые была предложена Форни как метод получения высокоэффективного кода посредством комбинации двух или более компонуемых (составных) кодов. В результате, такие коды могут корректировать ошибки в значительно более длинных кодах и имеют структуру, которая позволяет относительно легко осуществить декодирование средней сложности. Последовательные каскадные коды часто используются в системах с ограничением мощности, таких как космические зонды. Самая распространенная из этих схем содержит внешний код Рида — Соломона (выполняется первым, убирается последним), который следует за свёрточным внутренним кодом (выполняется последним, убирается первым). Туброкоды могут быть последовательными и параллельными с последующей конкатенацией (объединением) результатов. Кодирование производится как итерационными, так и рекурсивными методами.
Декодирование турбокодов производится методами аналогичными методам декодирования свёрточных кодов. Здесь имеет место быть принцип максимума апостериорной вероятности (англ. maximum a posteriori, MAP). Аналогом алгоритма Витерби при турбокодирование являются алгоритмы Бала или его модификация — алгоритм Берру.
Наличие нескольких декодеров в составе декодера турбокода позволяет осуществлять, так называемую, обратную связь декодирования, которая позволяет влиять результатам декодирования одного декодера на результаты другого.
Методы приёма сигналов
[править]Приём сигналов базируется на следующем утверждении: принимая любой сигнал, мы обязательно что-то о нём знаем и чего-то не знаем. Предварительные сведения о сигнале используются для рационального выбора метода приёма в соответствии с поставленными целями. Если бы о сигнале заранее не было известно абсолютно ничего, то его нельзя было бы принять, так как не известно было бы, чем сигнал отличается от несигнала, в частности, от любой помехи.
То, чего мы заранее не знаем, может являться носителем полезной информации. Если бы о сигнале нам абсолютно все было известно наперед, то такой сигнал не нужно было бы и передавать: он не принес бы нам никакой информации.
Говоря конкретно, объектом априорного знания или незнания могут являться те или иные физические параметры сигнала, например, интенсивность, несущая частота, время появления, длительность, и так далее.
Некоторые из этих параметров остаются неизменными. В таком случае их следует рассматривать как постоянные признаки сигнала, и наличие этих признаков нужно наилучшим образом использовать для различения сигнала и помехи.
Другие же параметры можно так или иначе модулировать. Эти параметры называются информационными. В их изменениях, неизвестных заранее на приёмной стороне, заложена переносимая сигналом информация. Обычно известен лишь диапазон возможных изменений информационных параметров.
В зависимости от назначения сигналов, задачи приёма сводятся к трём основным:
- обнаружение сигнала;
- различение сигналов;
- восстановление сообщения.
Обнаружение сигнала
[править]Под обнаружением (детектированием) сигнала понимается установление его наличия. При наличии шума (аддитивной помехи) задача сводится к получению ответа на вопрос — имеется ли на входе приёмника сигнал плюс шум, или только шум?
Кратко, обнаружение сигнала — это констатация наличия сигнала.
Часто ошибочно полагают, что обнаружение сигнала не требует измерения каких-либо параметров сигнала. Всякое обнаружение неразрывно связано с измерением тех или иных параметров. Более того: обнаружение это, в сущности, и есть измерение, хотя и грубое. В самом деле: когда обнаруживают сигнал, то обнаруживают его не вообще, а в определённой полосе частот, в определённом интервале времени и так далее. Интервалы, в которых заключены значения этих параметров, определяют точность, с которой они измеряются. В дальнейшем, если требуется, точность может быть повышена.
Если имеется возможность обнаружить сигнал, то есть отличить наличие сигнала от его отсутствия, то это открывает возможность передачи любой информации при помощи двоичного кода. Наличие сигнала (посылка) будет соответствовать символу 1, отсутствие сигнала (пауза) — символу 0. Такая система носит название передачи с пассивной паузой, так как в паузе передатчик бездействует.
В теории приёма-передачи данных важным понятием является «оптимальный приёмник», или применительно к поставленной задаче — «оптимальный обнаружитель». Под оптимальным обнаружителем понимается теоретически наилучший вид приёмника, позволяющий детектировать наличие заранее известного сигнала при максимальном уровне отношения «сигнал/помеха». В качестве такого может служить согласованный фильтр. Согласованный фильтр рассчитывается для обнаружения сигнала заранее известной формы, выходной сигнал фильтра при этом не совпадает по форме ни со входным, ни с сигналом, для обнаружения которого фильтр предназначен (кроме импульса с огибающей гауссовой формы). Сигнал, с которым фильтр согласован, детектируется однозначно, поскольку именно при его наличии во входном сигнале с шумом амплитуда выходного сигнала фильтра максимальна.[6]
Передаточная функция фильтра имеет вид:
где — амплитудно-частотная характеристика (АЧХ) фильтра;
— фазочастотная характеристика (ФЧХ) фильтра.
Для отыскания оптимальной передаточной функции, максимизирующей отношение «сигнал/помеха» на выходе фильтра при наличии помехи с равномерной спектральной плотностью мощности, необходимо составить отношение:
где — момент времени, в который наблюдается максимум выходного сигнала;
— пиковое значение сигнала на выходе фильтра;
— среднеквадратичное значение помехи на выходе фильтра;
— спектральная плотность сигнала.
Используя неравенство Буняковского — Шварца, получим:
где — полная энергия входного сигнала.
Неравенство (44) обращается в равенство при
где — произвольная постоянная;
— функция, комплексно-сопряженная с ,
Выражение (45) можно представить как
где — фаза спектральной плотности сигнала;
— модуль спектральной плотности сигнала.
Отношение (46) определяет передаточную функцию фильтра, обеспечивающего максимум отношения «сигнал/помеха» на выходе.
Из принципа физической реализуемости согласованного фильтра следует, что время достижения максимального сигнала на выходе фильтра равно длительности импульса .
Для того чтобы достоверно говорить об обнаружении сигнала в смеси «сигнал+шум», необходимо, чтобы выполнялось неравенство[7]:
где — некое пороговое значение напряжения, конкретно заданное для каждого вида сигнала.
Пороговое напряжение определяется как:
где — энергия смеси «сигнал+шум»;
— энергия сигнала;
— косинус угла при вершине конуса, образованного векторами системы сигналов.
Например, для ортогональных сигналов . Таким образом, для определения наличия сигнала в смеси, нужно наличие положительного потенциала на выходе согласованного фильтра в момент времени .
Различение сигналов
[править]При передаче двух различных сигналов, и , положение несколько иное. Здесь речь идёт уже не об обнаружении, а о различении двух сигналов. Дело сводится к ответу на вопрос: имеется ли на входе приёмника сигнал плюс шум, или сигнал плюс шум? Ответ на этот вопрос определяется уже не свойствами каждого сигнала в отдельности, эти свойства в принципе могли бы оставаться неизвестными, а физическим различием между сигналами. Сигналы могут различаться между собою значениями тех или иных параметров. При выборе двух сигналов нужно стремиться к тому, чтобы различие между ними было по возможности более стойким по отношению к действию помехи. Это значит, прежде всего, что различие должно быть по возможности велико, с тем, что если оно уменьшится в процессе передачи под действием помехи, то оставшееся различие должно быть все же достаточно для уверенного различения сигналов. Но, кроме того, нужно выбирать различие по тому параметру (из всех параметров данного сигнала), который в наименьшей степени подвержен влиянию помехи данного типа.
Очевидно, случай обнаружения может рассматриваться как вырожденный случай различения двух сигналов, когда один из них есть тождественный нуль.
Передача двоичным кодом, в котором символу 1 соответствует сигнал , а символу 0 — сигнал , называется передачей с активной паузой.
Случай различения многих сигналов в принципиальном отношении мало отличается от случая различения двух сигналов. Все сказанное выше по поводу различения двух сигналов должно быть отнесено в случае набора из нескольких сигналов к любой паре сигналов, входящих в этот набор. Однако техника различения многих сигналов может оказаться существенно отличной от техники различения двух сигналов.
Восстановление сигналов
[править]Задача восстановления сообщения значительно отличается от задач обнаружения и различения сигналов. Она состоит в том, чтобы получить выходной сигнал , наименее отличающийся от передаваемого сообщения . При этом существенно, что сообщение заранее неизвестно; известно лишь, что оно принадлежит к некоторому множеству. При таких условиях можно рассматривать данное сообщение как одну из реализаций некоторого случайного процесса. Следовательно, заранее известными могут быть только распределения или моменты распределения этого процесса. В частности, на приёмной стороне могут быть заранее известны мощность и спектр случайного процесса, реализацией которого является передаваемое сообщение. Борьба с помехами при такой постановке задачи, конечно, более трудна.
При восстановлении сообщения нужно опираться на некоторый критерий верности, на основе которого оценивается уклонение выходного сигнала от передаваемого сообщения . Этот критерий должен, вообще говоря, выводиться из требований, предъявляемых к передаче данного вида сообщений.
Существует несколько критериев верности:
- Часто применяется критерий квадратичного уклонения. Для непрерывных функций, заданных на интервале , квадратичное уклонение выражается соотношением:
- Можно применить критерий абсолютного уклонения:
- Можно также воспользоваться критерием наибольшего уклонения:
Нет решительно никаких общих оснований для предпочтения одного критерия другому. Критерий квадратичного уклонения применяется особенно часто только потому, что при пользовании этим критерием получаются, как правило, сравнительно простые выкладки.
Если получателем сообщения является человек, то критерий верности должен, естественно, выбираться на основе свойств восприятия человеком данного вида сообщений. Так, например, при передаче звука критерий верности должен строиться на основе психофизиологических свойств слуха, а при передаче изображений — на основе свойств зрения.
Если непрерывное сообщение вырабатывается некой телеметрической системой и отображает изменение во времени наблюдаемой физической величины, то критерий верности сводится к точности измерения, требования к которой выводятся из общего назначения данного измерения и условий применения его результатов.
Понятие помехоустойчивости
[править]Основы теории помехоустойчивости заложены В. А. Котельниковым в работе «Теория потенциальной помехоустойчивости»[8] (1956). В этой работе впервые поставлены и решены многие основные задачи и введён ряд фундаментальных понятий. Она с полным основанием считается классическим исследованием проблемы помехоустойчивости.
Помехоустойчивость технического устройства (системы) — способность устройства (системы) выполнять свои функции при наличии помех. Её оценивают интенсивностью помех, при которых нарушение функций устройства ещё не превышает допустимых пределов.[9] Эта общая формулировка должна быть уточнена применительно к различным условиям передачи, то есть должна быть установлена количественная мера помехоустойчивости.
Прежде всего, помехоустойчивость понимается как свойство системы передачи в целом. Но из-за сложности данной задачи имеет смысл говорить о помехоустойчивости отдельных звеньев системы. Так, можно говорить о помехоустойчивости кодов, о помехоустойчивости видов модуляции, о помехоустойчивости приёмников. При этом часто достаточно оперировать сравнительной или относительной помехоустойчивостью, что позволяет сравнить между собою различные варианты технических решений.
Требования к помехоустойчивости различных устройств отличаются большим разнообразием: так, в радиолокационных системах иногда считают допустимым пропуск отдельных радиолокационных станцией (за время однократного обзора контролируемой ею области пространства) до половины объектов, подлежащих обнаружению, а в системах передачи данных, использующих ЭВМ, часто недопустима потеря даже одного передаваемого бита из порядка .
Предельно достижимая помехоустойчивость называется, по В. А. Котельникову, потенциальной помехоустойчивостью. Сравнение фактической помехоустойчивости каждого конкретного устройства с его потенциальной помехоустойчивостью даёт оценку качества устройства и показывает наличие ещё неиспользованных резервов.
Действие помехи проявляется в том, что принятый сигнал (а следовательно, и сообщение) отличается от переданного. Поэтому помехоустойчивость можно характеризовать как степень соответствия принятого сигнала (или сообщения) переданному при заданной помехе. Таким образом, при сравнении нескольких систем та из них будет более помехоустойчивой, в которой при одинаковой помехе различие между принятым и переданным сигналами (или сообщениями) будет меньше.
Ввести единое количественное определение помехоустойчивости затруднительно, так как критерий соответствия принятого сигнала переданному и характеристики действующей в системе помехи могут в зависимости от условий передачи существенно различаться.
Вместе с тем оказывается полезным ввести определение меры соответствия принятого сигнала переданному. С одной стороны, эта мера зависит от помехи, и характеризует помехоустойчивость с необходимой полнотой. С другой стороны, эта мера, взятая не как функция помехи, а как численный показатель системы, работающей в заданных условиях, представляет собой показатель, вполне характеризующий систему с точки зрения потребителя.
Для обозначения степени соответствия принятого сообщения переданному используют термин верность. Количественную меру соответствия выбирают в зависимости от характера сообщения: дискретный или непрерывный.
Рассмотрим первый случай. Пусть сообщение представляет собой последовательность символов из некоторого ансамбля (то есть конечного множества, заданного вместе с априорными вероятностями его элементов). В этом случае влияние помехи проявляется в том, что вместо фактически переданного символа принимается какой-либо другой. Такое событие называют ошибкой. Так как ошибка есть случайное событие, то верность естественно характеризовать вероятностью отсутствия ошибки, то есть вероятностью правильного приёма. Если вероятность ошибки обозначена , то вероятность правильного приёма
На практике мера верности или, верность выражается положительным числом , определяемым как:
В случае передачи непрерывных функций нельзя столь же легко ввести количественную меру верности, так как в этом случае нет простой системы событий (ошибка есть — ошибки нет). При передаче непрерывного сообщения отличие принятого сообщения от переданного имеет также непрерывный характер. Поэтому мерой несоответствия или уклонения может служить некоторая величина , представляющая собой расстояние между принятым и переданным сообщениями, или критерий верности, рассмотренный ранее.
Количественную меру верности вводят, определив её возрастающей функцией вероятности:
то есть вероятности того, что уклонение не превзойдёт некоторой заранее назначенной величины .
Выясним связь между верностью и отношением «сигнал/помеха».
Верность тем ниже, чем больше относительная интенсивность помехи, то есть чем меньше отношение «сигнал/помеха», или верность есть возрастающая функция отношения «сигнал/помеха». Но что отношение «сигнал/помеха» — не единственный фактор, влияющий на верность. Во-первых, при неизменной мощности сигнала можно выбирать разные системы сигналов — строить множество сигналов с различными расстояниями между элементами этого множества. Выбор расстояний должен быть таков, чтобы помеха с заданными свойствами в наименьшей степени влияла на различимость принятых сигналов. В простейшем случае дело сводится к построению системы сигналов с наибольшими расстояниями. Во-вторых, верность зависит от способа приёма, так что она может быть различной при одном и том же отношении «сигнал/помеха». Часто отношение «сигнал/помеха» в некотором звене приёмника больше, чем то же отношение на входе приёмника. Канал же характеризуется именно отношением «сигнал/помеха» на выходе линии, то есть на входе приёмника. Правильно сконструированный приёмник может увеличить отношение «сигнал/помеха», и притом весьма значительно.
Как уже было сказано выше, следует говорить о помехоустойчивости отдельных звеньев системы передачи.
Под помехоустойчивостью кода нужно понимать верность при заданном отношении «сигнал/помеха» и при определённом способе приёма.
Помехоустойчивость системы модуляции непосредственно характеризуется относительным изменением модулируемого параметра под действием данной помехи. Можно сравнивать различные системы модуляции по относительному увеличению отношения «сигнал/помеха», даваемому некоторым идеализированным приёмником.
Помехоустойчивость приёмника также удобно выражать относительным увеличением отношения «сигнал/помеха», сравнивая значение этого отношения на выходе звена приемника, производящего основную обработку сигнала, со значением того же отношения на входе приёмника.
Более широким понятием, чем помехоустойчивость, является помехозащищённость. Это способность системы связи противостоять воздействию мощных помех. Помехозащищённость включает в себя скрытность системы связи и ее помехоустойчивость, так как для создания мощных помех надо сначала обнаружить систему связи и измерить основные параметры её сигналов, а затем организовать мощную, наиболее сильнодействующую помеху. Чем выше скрытность и помехоустойчивость, тем выше помехозащищённость системы связи.
Литература
[править]- Бойерле, Х. П., Беценар, Г. Бах Коммуникация в технике автоматизации. — Пер. с нем. — Берлин, Мюнхен: АО Siemens, 1991. — 155 с. — ISBN 3-8009-1563-4.
- Варакин, Л. Е. Теория систем сигналов. — М.: Советское радио, 1978. — 375 с.
- Гоноровский, И. С. Радиотехнические цепи и сигналы: Учебник для вузов. — 4-е изд., перераб. и доп. — М.: Радио и связь, 1986. — 512 с.
- Гук, М. Аппаратные средства локальных сетей. Энциклопедия. — Спб.: Питер, 2000. — 576 с. — ISBN 5-8046-0113-X.
- Защита от радиопомех / Под ред. М. В. Максимова. — М.: Советское радио, 1976. — 496 с.
- Зимин, В. В. Промышленные сети: Учеб. пособие для студентов вузов. — Н. Новгород: НГТУ им. Р. Е. Алексеева, 2008. — 252 с. — ISBN 978-5-93272-554-2.
- Олифер, В. Г., Олифер, Н. А. Компьютерные сети. Принципы, технологии, протоколы: Учебник для вузов. — 3-е изд. — СПб.: Питер, 2006. — 958 с. — ISBN 5-469-00504-6.
- Осмоловский, С. А. Стохастические методы передачи данных. — М.: Радио и связь, 1991. — 240 с.
- Отт, Г. Методы подавления шумов и помех в электронных системах / Пер. с англ. — М.: Мир, 1979. — 318 с.
- Скляр, Б. Цифровая связь. Теоретические основы и практическое применение / Пер. с англ. — 2-е изд, испр. — М.: Издательский дом «Вильямс», 2003. — 1104 с. — ISBN 5-8459-0497-8.
- Таненбаум, Э. Компьютерные сети. — 4-е изд. — Спб.: Питер, 2003. — 992 с. — ISBN 5-318-00492-X.
- Трахтман, А. М., Трахтман, В. А. Основы теории дискретных сигналов на конечных интервалах. — М.: Советское радио, 1975. — 208 с.
- Тузов, Г. И. Статистическая теория приёма сложных сигналов. — М.: Советское радио, 1977. — 400 с.
- Финк, Л. М. Теория передачи дискретных сообщений. — 2-е изд., перераб. и доп. — М.: Советское радио, 1970. — 728 с.
- Харкевич, А. А. Борьба с помехами. — 2-е изд., доп. и перераб. — М.: Наука, 1965. — 276 с.
- Хармут, Х. Ф. Передача информации ортогональными функциями. — М.: Связь, 1975. — 272 с.
- Хелд, Г. Технология передачи данных. — 7-е изд. — СПб.: Питер, 2003. — 720 с. — ISBN 5-94723-472-6.
Примечания
[править]- ↑ Варакин, Л. Е. Теория систем сигналов. — М.: Советское радио, 1978. — 375 с.
- ↑ Отт, Г. Методы подавления шумов и помех в электронных системах / Пер. с англ. — М.: Мир, 1979. — 318 с.
- ↑ а б в Зимин, В. В. Промышленные сети: Учеб. пособие для студентов вузов. — Н. Новгород: НГТУ им. Р. Е. Алексеева, 2008. — 252 с. — ISBN 978-5-93272-554-2.
- ↑ Таненбаум, Э. Компьютерные сети. — 4-е изд. — Спб.: Питер, 2003. — 992 с. — ISBN 5-318-00492-X.
- ↑ Гук, М. Аппаратные средства локальных сетей. Энциклопедия. — Спб.: Питер, 2000. — 576 с. — ISBN 5-8046-0113-X.
- ↑ Гоноровский, И. С. Радиотехнические цепи и сигналы: Учебник для вузов. — 4-е изд., перераб. и доп. — М.: Радио и связь, 1986. — 512 с.
- ↑ Харкевич, А. А. Борьба с помехами. — 2-е изд., доп. и перераб. — М.: Наука, 1965. — 276 с.
- ↑ Котельников, В. А. Теория потенциальной помехоустойчивости. — М.: Госэнергонздат, 1956. — 152 с.
- ↑ Кобзарев, Ю. Б. Помехоустойчивость / БСЭ. — 3-е изд. — М.: Большая советская энциклопедия, 1974. — Т. 46.





















![{\displaystyle M[\xi (t)\xi (t+\tau )]=\int \limits _{-\infty }^{+\infty }\int \limits _{-\infty }^{+\infty }x_{1}x_{2}w(x_{1},\;x_{2})\,dx_{1}dx_{2}=R(\tau ).\qquad \qquad (9)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/946a35881c303790b3e85d91a61ef20e6b6b957c)























































































































































































![{\displaystyle \varepsilon _{2}=\int \limits _{a}^{b}[x(t)-y(t)]^{2}\,dt.\qquad \qquad (49)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81cefda59b0d122898cb69469e8e2edf891f4e34)








