История Биткоина/Урок 2. История создания алгоритма SHA-256

Создание хэш сумм.

Хэш-суммы, или криптографические хэш-функции, являются неотъемлемой частью сети Биткойн. Они играют решающую роль в процессе майнинга и обеспечении безопасности блокчейна. При добыче биткоинов майнеры соревнуются в решении сложных математических головоломок, чтобы подтвердить и добавить новые блоки транзакций в блокчейн. Эти головоломки требуют значительных вычислительных мощностей и предполагают поиск конкретного хэш-значения, удовлетворяющего определенным критериям. Хэш-суммы используются для создания уникального цифрового отпечатка данных внутри каждого блока. В случае Биткоина используется хэш-функция SHA256.

Методы получения Хэш-суммы имеют длительную историю.Галилео Галилей наблюдал кольца Сатурна, которые принял за «ушки». Не будучи уверен, но желая утвердить свой приоритет, он опубликовал сообщение с перестановленными буквами: smaismrmilmepoetaleumibunenugttauiras. В 1610 году он раскрыл исходную фразу: Altissimum planetam tergeminum obseruaui, что в переводе с латинского языка означает «высочайшую планету тройною наблюдал». Таким образом, на момент публикации первого сообщения исходная фраза не была раскрыта, но была создана возможность подтвердить её позже.

В середине 1650-х Христиан Гюйгенс разглядел кольца и опубликовал сообщение с буквами, расставленными по алфавиту: aaaaaaacccccdeeeeeghiiiiiiillllmmnnnnnnnnnooooppqrrstttttuuuuu. Через некоторое время была опубликована и исходная фраза: Annulo cingitur, tenui plano, nusquam cohaerente, ad eclipticam inclinato — «Окружен кольцом тонким, плоским, нигде не подвешенным, наклоненным к эклиптике». От применения хеш-функции, включая и цель позднее подтвердить некоторое нераскрытое сообщение, данный случай отличается только тем, что выходное сообщение не имеет фиксированной длины, а определяется длиной входного. Фактически, расстановка букв исходного сообщения по алфавиту является некоторой хеш-функцией, но только с результатом нефиксированной длины.

В январе 1953 года Hans Peter Luhn (сотрудник фирмы IBM) предложил «хеш-кодирование». Дональд Кнут считает, что Ханс первым выдвинул систематическую идею «хеширования».

В 1956 году Arnold Dumey в своей работе «Computers and automation» первым описал идею «хеширования» такой, какой её знает большинство программистов сейчас. Думи рассматривал «хеширование» как решение «проблемы словаря», предложил использовать в качестве «хеш-адреса» остаток от деления на простое число.

В 1957 году в журнале «IBM Journal of Research and Development» была опубликована статья Уэсли Питерсона о поиске текста в больших файлах. Эта работа считается первой «серьёзной» работой по «хешированию». В статье Уэсли определил «открытую адресацию», указал на уменьшение производительности при удалении. Спустя шесть лет была опубликована работа Вернера Бухгольца, в которой было проведено обширное исследование «хеш-функций». В течение нескольких последующих лет «хеширование» широко использовалось, однако никаких значимых работ не публиковалось.

В 1967 году «хеширование» в современном значении упомянуто в книге Херберта Хеллермана «Принципы цифровых вычислительных систем». В 1968 году Роберт Моррис опубликовал в журнале «Communications of the ACM» большой обзор по «хешированию». Эта работа считается «ключевой» публикацией, вводящей понятие о «хешировании» в научный оборот, и закрепившей термин «хеш», ранее применявшийся только специалистами (жаргон).

Создание алгоритма SHA-256

Односторонняя функция сжатия $f$, преобразует два входных блока фиксированной длины в выходной блок того же размера, что и входные; алгоритм начинает с вектора инициализации IV, функция $f$ выполняется последовательно над результатом каждого предыдущего прохода

В 1979 году в докторской диссертации Ральфа Меркла. Меркл и Дамгор независимо показали: если функция сжатия устойчива к коллизиям, то и хеш-функция будет также устойчива — чтобы доказать устойчивость структуры, сообщение дополняется блоком, который кодирует длину первоначального сообщения (упрочнение Меркла — Дамгора). Структура предусматривает вектор инициализации — фиксированное значение, которое зависит от реализации алгоритма, и которое применяется к первому проходу — применению функции сжатия f к нему и первому блоку сообщения. Результат каждого прохода передаётся на следующий вход f и очередному блоку сообщения; последний блок дополняется нулями, если необходимо, также, добавляется блок с информацией о длине целого сообщения. Для упрочнения хеша последний результат иногда пропускают через функцию финализации (англ. finalisation function), которая может использоваться также для уменьшения размера выходного хеша сжатием результата последнего применения f в хеш меньшего размера или чтобы гарантировать лучшее смешивание битов и усилить влияние небольшого изменения входного сообщения на хеш (обеспечить лавинный эффект). Функция финализации часто строится с использованием функции сжатия.

В 1991 году на базе данных теоретических работ был разработан алгоритм MD5, что расшифровывается message digest(подпись сообщения). В отличие от исторических хэш сумм подпись сообщения как правило намного короче, чем исходное сообщение. MD5 оперирует данными в 512-битных блоках и выдает 128-битное хэш-значение. Он использует серию логических операций, побитовых операций и модульную арифметику для обработки входных данных и генерации хэш-вывода. Результирующее хэш-значение уникально для входных данных, а это означает, что даже небольшое изменение входных данных приведет к значительно отличающемуся хэш-значению.

Первоначально MD5 получил широкое распространение и стал одной из наиболее часто используемых хэш-функций. Он нашел применение в различных областях, включая цифровые подписи, контрольные суммы и проверку целостности данных. Однако со временем исследователи обнаружили значительные уязвимости в MD5. В 1996 году в алгоритме MD5 были обнаружены коллизии (разные входные данные, выдающие один и тот же хэш-результат). По мере того как слабые места в системе безопасности становились все более заметными, стало ясно, что MD5 больше не подходит для приложений, требующих высокой устойчивости к коллизиям, таких как центры сертификации и цифровые подписи.

На смену ему агентством национальной безопасности США (NSA) был разработан алгоритм SHA-1, что расшифровывается как Secure Hash Algorithm. Он был опубликован в 1995 году национальным институтом стандартов и технологий (NIST). SHA-1 оперирует данными в 512-битных блоках и выдает 160-битное хэш-значение. В течение многих лет SHA-1 был широко распространен и стал одной из наиболее часто используемых хэш-функций. Он был интегрирован в многочисленные протоколы безопасности и приложения, включая SSL/TLS, HTTPS и различные алгоритмы цифровой подписи.

Схема одной итерации алгоритмов SHA-2

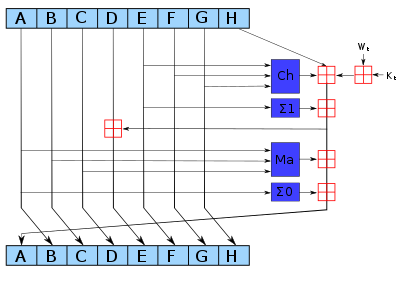
Однако со временем исследователи обнаружили уязвимости в SHA-1, которые вызвали опасения по поводу его безопасности. В 2004 году были опубликованы теоретические атаки на SHA-1, в которых подчеркивался потенциал коллизионных атак. Столкновение происходит, когда два разных входных сигнала выдают один и тот же хэш-вывод, что подрывает свойства безопасности хэш-функции. По мере увеличения вычислительной мощности и совершенствования криптографических методов исследователи добились значительного прогресса в практических коллизионных атаках против SHA-1. В 2005 году теоретическая атака снизила сложность поиска столкновения с 2^80 до 2^69. Последующие атаки еще больше снизили сложность, сделав поиск коллизий все более выполнимым.

В 2001 году NIST опубликовал семейство алгоритмов SHA-2. При этом разработка алгоритма началась в конце 1990-х годов как усовершенствование существующего алгоритма SHA-1. В частности алгоритмы включали в себя SHA-224, SHA-256, SHA-384, SHA-512. Последняя цифра означает длину подписи сообщения. Для алгоритмов SHA-224, SHA-256 длинна блока составляла 512 бит, а для остальных 1024 бита. Алгоритм получил широкое распространение и стал широко использоваться в различных криптографических приложениях, включая цифровые подписи, хеширование паролей и проверку целостности данных.

Литература

• Брюс Шнайер Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. — М.: Триумф, 2002. — ISBN 5-89392-055-4
• Дональд Кнут Искусство программирования. Том 3. Сортировка и поиск = The Art of Computer Programming, vol.3. Sorting and Searching. — 2-е издание. — М.: «Вильямс», 2007. — С. 824. — ISBN 0-201-89685-0
• Никлаус Вирт Алгоритмы и структуры данных. — М.: «Мир», 1989. — ISBN 5-03-001045-9
• Никлаус Вирт Алгоритмы и структуры данных. Новая версия для Оберона. — М.: «ДМК Пресс», 2010. — ISBN 978-5-94074-584-6