Трудные темы курса физики/Силы инерции

Силы инерции
[править]Лекция (черновик)
Введение
[править]Трудные темы курса физики выявляются в практике преподавания курса физики в учебных заведениях любого уровня — институте, специализированном техникуме или средней школе, где успех зависит не только от внятности изложения материала и донесения его до обучающихся. Для этого от них требуется внимание и хорошая память. Проблема состоит в том, чтобы полученные ими знания превратились в умение. То есть способность оторваться от конспекта лекций или страниц учебника и самостоятельно принять ответственное решение применительно к заведомо не рассмотренному в процессе преподавания конкретному случаю.
Это требует активного участия обучаемых в формировании каждым применительно к своим способностям, склонностям и полученного персонального опыта и знаний личного взгляда на предмет обучения.
Лучшим способом достижения успеха в этом процессе является решение задач. Именно сравнение собственного решения с ответом и анализ того, почему он не сошёлся, и есть верный путь к пониманию предмета.
Отличительной чертой работ успешных преподавателей является то, что они намеренно предвосхищают возникающие по ходу изложения материала у своих учеников трудности и путём подробного, без потери мелких деталей, повествования, добиваются создания прочной базы понимания преподаваемого предмета.
В ряде случаев они используют весьма эффективный педагогический приём, подводя усыплённого гладко идущем повествованием читателя к кажущемуся парадоксу, заставляя его активно включиться в осмысление материала и строить свою картину, связанную с личными особенностями восприятия закономерностей окружающего мира.
Справедливости ради следует заметить, что человеку свойственно ошибаться и потому нельзя ожидать, что в текстах даже самых авторитетных авторов не могут встречаться досадные ошибки. Так, например, в цитируемой ниже глубокой работе профессора Хайкина С.Э. ([1] стр 205-208)рассматривается в частности вопрос о падении камня на Землю. Ради обострения ситуации автор рассматривает и вопрос о падении Земли на камень и делает существенную ошибку, ставящую под сомнение полученные им в данном вопросе выводы.Ошибка заключается в том, что и камень, и Земной шар в действительности падают на общий центр притяжения и потому путь, проходимый Землёй не равен пути, проходимому камнем.
Поэтому постоянная бдительность читателя и критическое отношение к суждениям авторитетов, независимо от их ранга и степени, совершенно необходимы в том случае, если он действительно задался целью понять физику. В большинстве случаев такой скептицизм позволит обнаружить неполноту и ошибки в собственных знаниях. Однако, в редких случаях и уважаемые учёные способны удивить читателя.
От ошибок и ухода в область фантазии предохраняет бескомпромиссный принцип, сформулированный ещё Бэконом, заключающийся в том, что единственным критерием научной истины является опыт. При этом научная концепция может подтверждаться множеством опытов, но достаточно лишь одного, где она не срабатывает, чтобы поставить всю эту концепцию по крайней мере, под сомнение.
Иная картина наблюдается в тех случаях, где приходится обращаться к вопросам философским, затрагивающих проблему не применения, но происхождения используемых на практике понятий физики.Здесь следует отличать во многом философскую проблему определения понятия, как такового, от вопроса возникновения в конкретных условиях опыта той или иной физической величины, описываемых данным понятием.
В начале 20 столетия классическая наука переживала серьёзный кризис и естественным ответом на него стало появление эмпириокритицизма, известного также по имени физика Эрнста Маха, одного из создателей этого направления, как Махизм. Одним из основ его теории был Принцип экономии мышления, из которого следовало, что объяснительная функция науки, основанная на поисках причин того или иного наблюдаемого на опыте явления, является излишней и должна быть исключена. Науке по Маху следует отказаться от попыток объяснения причин возникновения этих эффектов. И потому физические понятия (в том числе и понятие о силах инерции) и связанные с ними термины, являются не более, чем удобным средством описания наблюдаемых физических явлений.
Сходная точка зрения встречается и в современных курсах механики. Так, например, не редко приходится встретить утверждение, что силы инерции, (точнее эйлеровы силы инерции), не существуют в действительности, но представляют собой искусственное понятие, вводимое по воле человека ради формальной возможности и удобства записи им уравнений движения тел в неинерциальных системах отсчёта.[2].Следует признать , что весьма большое количество авторов учебников по механике как в России, так и за рубежом придерживаются сходной ориентации во взглядах на силу инерции.
Понятие о силе инерции имеет прямое отношение к основам современной физики, поскольку именно наличие этих сил даёт основание сказать, является ли система координат, в которой происходит механическое движение, инерциальной или же не инерциальной. Точнее: можно ли рассматривать заданную систему координат инерциальной потому, что действующие в ней силы инерции не превышают наперёд заданной величины, в свою очередь зависящей от величины допустимой ошибки результата.
Существенный вклад в новейшие представления о сущности времени внесла Специальная теория относительности (СТО), которая имеет дело с движением тел в одной из множества инерциальных систем.
Ещё более революционной оказалась Общая теория относительности (ОТО),предметом которой является движение в ускоренно движущихся системах координат, то есть в системах неинерциальных
Однако вопрос о сущности сил инерции, чрезвычайно осложнён недомолвками и подчас полным непонимания того, что представляет собой феномен инерции и сопровождающих его сил. Многие сходятся на том, что в основе возникающих трудностей лежит нечёткая и неоднозначная терминология, а в термин «сила инерции» вкладывается разное содержание.(Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — С. 15. — 320 с.)
Вопрос о путанице начинается с каламбура, в соответствие с которым инерциальной системой называются системы, в которых не действуют силы инерции, а неинерциальной - те, отличительной чертой которых является существование сил инерции, величиной которых нельзя пренебречь.
Отсутствие прогресса в создании определённости связано с тем, что система взглядов на пространство, время и движение входит в основу мировоззрения мыслящего субъекта и, поскольку взгляды людей имеют специфические особенности, нельзя ждать полного единства мнений и в вопросе объяснения явления инерции.К тому же поколения сменяются и новое поколение, сменившее сумевшее разобраться в вопросе, наследует знания и ошибки предшествующего.
И потому автор выдержавшего три издания учебника Механики Хайкин С.Э. проявив свою способность заглядывать в будущее, высказав мнение, что устранение широко распространённых заблуждений, вызванных дефектами терминологии «представляет собой задачу, почти безнадёжную» (Хайкин, Семён Эммануилович. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы. стр. 3).
В своих сочинениях по механике, в том числе по обсуждаемой здесь книге, автор видит выход из создавшегося положения в отказе от бесплодного блуждания в области терминологии среди противоречащих друг другу мнений. Он полагается на здравый смысл и информированность читателя в рамках школьного курса физики. И считает, что читатель сам должен путём детального анализа физической картины самостоятельно уточнять терминологию при настолько детальном рассмотрении, чтобы дефекты терминологии выступили наиболее выпукло и очевидно. И только это позволит ему создать приемлемую для себя и при том адекватную действительности физическую картину явления или понятия.
Свою же роль, как педагога, автор видит в помощи читателя, снабжая его максимумом информации и обращая внимание на важные для понимания тонкости. Причём по возможности заменяя множество математических выражений гораздо большим количеством слов, объясняющих смысл этих выражений. При этом автора не смущает, что это ведёт к существенному увеличению объёма книги. Он надеется, что в случае, если такой подход позволит хотя бы частично устранить недоразумения в отношении силы инерции, то это увеличение объёма себя оправдает. ("Силы инерции и невесомость".Стр.4)
Рассмотрения вопроса о сути сил инерции будет вестись в близком соответствии методике, предложенной С.Э.Хайкиным
Законы движения
[править]В своих работах по механике автор уделял внимание понятийной стороне обсуждаемых положений, что приводило его к вторжению в область натурфилософии. Так он подробно обсуждал вопрос о принципиальной разнице в отношении понятия «физический закон» и «определение физической величины». Он настаивает, что во всякой формулировке положения следует ясно различать, что в нём является определением, а что -утверждением . Утверждение-это то, что может оказаться верным или неверным, т.е противоречащим опытным фактам. Только утверждение может стать физическим законом. Определение же неверным оказаться не может. Оно может оказаться непригодным или не целесообразным и только в этом отношении будет нуждаться в опытной проверке. При этом подчёркивает, что «физическое содержание всякого закона только тогда становится ясным, когда точно определены способы измерения всех физических величин, фигурирующих в математической формулировке закона»([1] . Стр. 88-89).
Обязательным при этом является независимое измерение входящих в закон величин
Oсновные понятия
[править]Си́ла — векторная физическая величина,характеризующаяся модулем и направлением [3] и являющаяся мерой интенсивности воздействия на данное тело других тел или полей. Независимо от причины своего возникновения, сила проявляет себя исключительно механически. А именно, будучи приложенной к массивному телу - контактные силы (и в этом случае можно говорить о точке приложения силы), сила становится причиной изменения параметров движения (направления или скорости) или возникновения в нём деформаций.([4]. Там же.) В случае воздействия на телу полей (гравитационного или электро-магнитного) имеет место распределение действующей силы по всему объёму тела и потому в этом случае говорить о точке приложения силы не имеет смысла ([1] Страницы 43 - 124)
Движение — Для того, чтобы описать движение тела,(или его части) необходимо выбрать другое тело или их совокупность, взаимное расположение которых в пространстве за время наблюдения не меняется. Мы связываем с ним/с ними некоторую систему координат (для большей конкретности декартову систему координаат) и рассматриваем движение, как изменение хотя бы одной проекции тела (в данном случае представляемого в виде материальной точки) на одну из координатных осей. Для будущего важно, что и носитель системы координат, также, как и наблюдаемое тело обладает массой .Массу же тела назовём
Масса — мера инертности тела.Понятие инерции было введено Ньютоном в его «Математических началах натуральной философии»([5]): «Врождённая сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает свое состояние покоя или равномерного прямолинейного движения», а собственно термин «сила инерции» был, по словам Леонарда Эйлера, впервые употреблён в этом значении Кеплер, Иоганн([5], со ссылкой на Е. Л. Николаи Страница 131).
Отголоском ньютоновского выбора термина «сопротивление» для описания инерции является также представление о некоей силе, якобы реализующей это свойство в форме сопротивления изменениям параметров движения. В связи с этим Максвелл, Джеймс Клерк заметил, что с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким, так как сладким оно становится не само по себе, а лишь после того, что в него положен сахар([5]Страница 130)
В современной науке существует только одна концепция, количественно определяющая связь между силой и вызываемым ею ускорением. Эта концепция воплощена в законах Ньютона.
Хайкин, со своей стороны, стойко придерживался материалистических взглядов на природу, и сторонился субъективного идеализма. В своих трудах неоднократно подчёркивал, что её законы не зависят от произвола человека. Он исходил из того, что Второй закон Ньютона в ускоренно движущихся система отсчёта «полностью сохраняет свою силу» ([1] Стр.133). Он писал, что с позиции общих принципов механики в отношении сил инерции (точнее эйлеровых сил инерции) «…следует признать, что у нас нет сколько-нибудь веских оснований сомневаться в реальности сил инерции…»([1] Стр.178)
Подробно рассмотрев определение сил инерции в различных неинерциальных систем координат, автор задаётся вопросом о происхождении сил инерции во вселенском масштабе.И здесь он вынужден обратиться к Принципу Маха(не называя его) и принимая, как гипотезу, утверждение, что своим происхождением силы инерции обязаны всему веществу Вселенной, находящееся за пределами Солнечной системы.Но оставляет этот вопрос нерешённым([1] Стр.169 - 178).
Терминология
[править]В российской литературе даётся такое определение силам инерции:
Векторная величина, равная произведению массы материальной точки на её ускорение и направленная противоположно ускорению, называется силой инерции [4].Страница 677
Такое определение содержит необходимое условие для того, чтобы назвать рассматриваемую силу силой инерции. Но оно недостаточно, поскольку использование этого термина применяется к трём различным силам, общим для которых является лишь название "сила инерции". А именно:
- силы-противодействия из третьего закона Ньютона («ньютонова сила инерции»[6]);
- силы, наблюдаемой при движении тела в неинерциальной системе отсчёта.Эта сила не имеет своего названия и будет здесь ради отличия её от ньютоновой и даламберовой называться просто силой инерции. Тем более, что именно эта сила наиболее часто используется и в отношении которой совершается основная масса недоразумений.
Хотя ввиду разнобоя в терминологии под этой силой иногда понимают лишь переносную силу инерции, возникающую вследствие прямолинейного и ускоренного движения движения системы координат в инерциальной системе отсчёта, наряду с другими формами неравномерности движения системы и наблюдаемого в ней тела. Вопрос о происхождении этой силы вызывает множество различных толкований.
Наличие, или отсутствие этой силы позволяет отличить Неинерциальную систему отсчёта (НСО) от Инерциальной системы отсчёта (ИСО).
- фиктивной (искусственно введённой и не являющейся следствием законов природы) силы, применяющейся в принципе Д’Аламбера («даламберова сила инерции»[6]).
Силы в законах Ньютона
[править]Рассмотрение движения тела без чёткого указания, в какой из этих систем происходит движение рассматриваемого тела невозможно.
Таким образом понятие о силе инерции неразрывно связано с тремя законами Ньютона.
Си́ла — векторная физическая величина,характеризующаяся модулем и направлением [7] и являющаяся мерой интенсивности воздействия на данное тело других тел или полей. Независимо от причины своего возникновения, сила проявляет себя исключительно механически. А именно, будучи приложенной к массивному телу - контактные силы (и в этом случае можно говорить о точке приложения силы) сила становится причиной изменения его скорости или возникновения в нём деформаций.([4]. Там же.) В случае воздействия на телу полей (гравитационного или электро-магнитного) имеет место распределение действующей силы по всему объёму тела и потому в этом случае говорить о точке приложения силы не имеет смысла ([1] Страницы 43 - 124)
Первый закон Ньютона
[править]Первый закон Ньютона вводит понятие инерциальных систем отсчёта ИСО :
Инерциальной системой будет называться такая система координат, в которой всякое тело будет сохранять состояние покоя или равномерного прямолинейного движения без вращения, пока и поскольку внешними силами оно не будет выведено из этого состояния
В механике нарушение описываемого движения связано с ускорением тела
Ньютон исходил из предположения, что инерциальные системы отсчёта объективно существуют и среди этих систем находится наиболее предпочтительная (сам Ньютон связывал её с эфиром, заполняющим всё пространство). Дальнейшее развитие физики показало, что такой системы нет, но это привело к необходимости выйти за пределы классической физики.
В роли инерциальной системы нередко используется координатная система, начало которой находится в Солнце. Однако уже появились сообщения, что вероятно и эта система движется в мировом пространстве с ускорением, величина которого составляет несколько единиц СИ после запятой.
Однако представление о возможности реализации Инерциальной системы отсчёта методически крайне необходимо , поскольку только благодаря введению такого допущения создаётся исходная предпосылка для дальнейшего рассмотрения вопроса о движении тела под действием приложенных к нему сил.Оправданием к правомочности такого положения является осознание, что в каждом конкретном случае можно выбрать такую систему отсчёта, в которой отступления от инерциальности будут меньше допустимых ошибок эксперимента.
Непосредственное измерение ускорения возможно с помощью акселерометра, простейшая схема которого приведена на Рис. 1
. Прибор представляет собой массивный груз, закреплённый между пружинами, другие концы которых присоединяются к телу, ускорение которого требуется измерить. При необходимости такой прибор снабжается системой регистрации смещения груза, пропорционального проекции ускорения тела на линию движения груза. При горизонтальном расположении прибора, когда единственная неуравновешенная пружинами сила является сила тяжести, направленная перпендикулярно возможному смещению и груз не испытывает ускорения, возможно выставить нуль отсчёта. При наличии постоянного ускорения в горизонтальном направлении и груз, сместившись, будет оставаться в новом стабильном положении, можно снова выставить указатель на нуль. В этом случае прибор сможет регистрировать неравномерность ускорения, если она будет иметь место.
Странно, что до сих пор приведённое выше определение вполне устраивает всех и никто не задаётся вопросом, в чём же будет выражаться это "Выведение из этого состояния". Или иначе; в чём конкретно заключается разница между Инерциальными системами и Неинерциальными системами. И как отличить одну от другой. Хотя ответ очевиден: признаком степени отступления от инерциальности является возникающая в этой системе сила инерции.Другие признаки есть лишь следствия этого положения
Второй закон Ньютона
[править]Отрицание универсальности Второго закона Ньютона имеет своим следствием отрицание реальности существования силы инерции.([1] Страницы 132 - 134)
В современной науке существует только одна концепция, количественно определяющая связь между силой и вызываемым ею ускорением. Эта концепция воплощена во втором законе Ньютона.
Второй закон заключается в утверждении, что между силой и вызываемым ею ускорением при рассмотрении движения тела в инерциальной системе отсчёта (ИСО) существует прямая пропорциональность, что записывается в виде:
= (1)
Существенно, что при формулировке своего закона Ньютон не касался природы и причин возникновения сил и ничем специально не ограничивал номенклатуру сил, действие которых рассматривается в этом законе.
Здесь входящий в коэффициент пропорциональности скаляр есть инертная масса. Этот закон часто записывают в такой форме:
= (2)
Применив тривиальный математический приём можно получить
- = 0 (3)
Как подчёркиается в ([5] Страница 186) из этой зависимости вовсе не следует , что вектор , имеющий размерность силы и совпадающий с ней по направлению есть сила, как самостоятельная физическая величина.
Существенно, что каждая из трёх входящих во Второй закон величин может быть определена самостоятельно и быть измерена с достаточной точностью, независимо от двух остальных. Именно поэтому выражения (1) и (2) выражают именно закон, но не способ определения той или иной входящей в него величины. ([1], Страница 88).
Но, поскольку (3)второй член слева не есть сила, (она не действует на рассматриваемое тело извне,то есть не является для рассматриваемого тела внешним и независимым от него фактором), то уравнение (3) не может быть истолковано, как компенсация действующих на тело посторонних сил , что с неизбежностью приводило бы на основании Второго закона к отсутствию ускорения. Что противоречило бы исходному положению о том, что тело движется с ускорением, пропорциональным действующей силе.([1] Страница 186) Отрицание универсальности Второго закона Ньютона имеет своим следствием отрицание реальности существования эйлеровой силы инерции.([3] Страницы 132 - 134)
Третий закон Ньютона
[править]Экспериментально доказано, что в инерциальной системе отсчёта в любом виде силового взаимодействия и независимо от того, меняется ли расстояние между телами и вообще движутся ли они, всегда выполняется условие:
(4)
То есть ускорения, сообщаемые телами друг другу, при взаимодействии двух тел направлены навстречу друг другу, и обратно пропорциональны массам тел.([1]Страница 96 )
Вводя в выражение (4) определения из Второго закона, приходим к общепринятой записи третьего закона Ньютона в его собственной формулировке:
Действию всегда есть равное и противоположное противодействие, иначе: взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны
([1]Страница 94 ) :
(5), или
= 0 (6)
После чего, составляя (3) и (6), находим
= - (7)
То есть второй член слева в (3) всё же есть сила, равная силе, ускоряющей тело, но приложенная не к нему, а к телу его ускоряющему,и в обратном направлении. Именно поэтому тело продолжает двигаться ускоренно, хотя в системе взаимодействующих тел имеется полная взаимная компенсация сил. В таком случае, прочтённое с точки зрения второго закона Ньютона выражение (6) означает, с одной стороны, что равнодействующая сил равна нулю и, следовательно, система из этих двух тел не двигается ускоренно. С другой стороны здесь не высказаны никакие запреты на ускоренное движение самих тел.
Дело в том, что понятие о равнодействующей возникает лишь в случае оценки совместного действия нескольких сил на одно и то же тело. В данном же случае, хотя силы равны по модулю и противоположны по направлению, но приложены к разным телам и потому, касательно каждого их рассматриваемых тел по отдельности, не уравновешивают друг друга, поскольку на каждое из взаимодействующих тел действует лишь одна из них. Равенство (6) не указывает на взаимную нейтрализацию их действия для каждого из тел, оно говорит о системе в целом.([1]Ссылка на Странице 94 на "Newton">Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989)
Механика Ньютона инвариантна по отношению к стреле времени — она допускает ход движения тел как в прямой, так и обратной по отношению ко времени последовательности. Однако в природе существует причинно-следственный порядок между происходящими событиями, в силу которого они располагаются в определённой последовательности во времени [9]. И поэтому при взаимодействии двух тел представляется логичным, что то из них, которое испытало ускорение, порождённое действием другого, считать пассивным, то есть ускоряемым, а другое — активным, то есть ускоряющим.[1].Страница 126 )
Дальнейшее рассмотрение вопроса ведётся с использованием графического представления сложного движения тела в некоторой системе отсчёта с началом в O', которая в свою очередь движется в исходной системе отсчёта с началом в O. ( Рис.2)Принято считать исходную систему отсчёта инерциальной и неподвижной, а подвижная система может двигаться относительно исходной без ускорения и тогда рассматриваться также как инерциальная, Так и с ускорением, т.е быть неинерциальной.Координаты тела в этих системах задаются радиус-векторами в виде :
(8)

Ньютонова сила инерции
[править]С учётом Рис.2 , и выражения (2) (выражающего второй закон Ньютона в инерциальной системе отсчёта и рассматривая движение тела в исходной (инерциальной системе), получаем :
(9)
Если есть результирующая всех реальных сил, действующих на тело, то это выражение, представляющее собой каноническую запись Второго закона, является просто утверждением, что получаемое телом ускорение пропорционально этой силе и массе тела.
Но выражение (9) может быть переписано в виде:
(10)
Для постороннего наблюдателя, находящегося в инерциальной системе и анализирующего ускорение тела, на основании сказанного выше такая запись имеет физический смысл только в том случае, если члены в левой части равенства относятся к силам, возникающим одновременно, но приложенным к разным телам. И в (10) второй член слева представляет собой такую же по величине силу, но направленную в противоположную сторону и приложенную к другому телу, а именно силу , то есть
(11)
В случае, когда оказывается целесообразным разделение взаимодействующих тел на ускоряемое и ускоряющее и, чтобы отличить действующие тогда на основании Третьего закона силы, те из них, которые действуют со стороны ускоряемого тела на ускоряющее называют ньютоновыми силами инерции ([5] страница 130 ), что соответствует записи выражения (5) для Третьего закона в новых обозначениях:
(12)
Существенно, что сила действия ускоряющего тела на ускоряемое и сила инерции имеют одно и то же происхождение и, если массы взаимодействующих тел близки друг другу настолько, что и получаемые ими ускорения сравнимы по величине, то введение особого наименования «сила инерции» является лишь следствием достигнутой договорённости. Оно так же условно, как и само деление сил на действие и противодействие.И наименования сил могут поменяться местами.Следовательно, Ньютонова сила инерции ничем не отличается от силы, действующей на тело и потому столь же реальна, как и эта действующая сила. ([1]Страница 178, 18-я строка сверху )
В случае, когда массы взаимодействующих тел несравнимы между собой (человек и твёрдый пол, отталкиваясь от которого он идёт). В этом случае деление тел на ускоряющие и ускоряемые становится вполне отчётливым, а ускоряющее тело может рассматриваться как связь, ускоряющая тело, но не ускоряемая сама по себе.
Эта связь не всегда может быть механической, то есть образованной силами деформации, возникающими при механическом контакте тел. Она может проявляться и при взаимодействии тел через создаваемые ими поля.
В любом случае ньютонова силы инерции приложена не к ускоряемому телу, а к связи.Поэтому она в уравнения движения не входит.
Просто сила инерции
[править]Все реально существующие системы отсчёта в принципе неинерциальны и во всех в принципе действуют реально существующие силы инерции.[1]. Хотя это утверждение не запрещает возможности вводить для удобства в рассмотрение заведомо фиктивную инерциальную систему, что позволяет существенно упростить и сделать наглядным проводимые рассуждения.
Общим для всех этих сил является то, что они подчиняются упомянутым выше законам Ньютона и равны массе тела, умноженной на переносное ускорение, которое заимствуется у материального тела, являющегося носителем неинерциальной системы отсчёта, в которой в ряде случаев может двигаться тело, испытывающее в этом случае относительное ускорение.Это ускорение равно нулю, если наблюдаемое тело неподвижно в неинерциальной системе отсчёта.
Направление силы инерции всегда противоположно действию силы, вызывающей ускоренное движение тела отсчёта. Следует обратить внимание, что эта сила по своей величине никак не связана с силой инерции, но представляет собой её материальную причину.Это обстоятельство, кстати, даёт основание заявлять, что в неинерциальных системах Третий закон Ньютона в отношении сил инерции не выполняется.
Здесь есть смысл рассмотреть два крайних случая:
I Сила действует по прямой линии, вследствие чего начало системы координат движется ускоренно по прямой, а само несущее её тело также имеет прямолинейную траекторию в любой ИСО. Дополнительным условием является предположение, что это тело не вращается
Характерной особенностью этого случая является то, что сила совершает работу по увеличению кинетической энергии несущего тела
II Сила действует под прямым углом к касательной в любой точке траектории.Это заставляет выделить из всех возможных ИСО только одну, в которой несущее систему координат вращается вокруг центра вращения, который может находиться как вне, так и внутри него.Центр вращения при этом считается неподвижным в ИСО.
Характерной особенностью этого случая является то, что сила не совершает работы и несущее тело сохраняет свой момент количества движения. Однако, как вариант здесь может быть рассмотрен случай неравномерного вращения
Но в каждом из этих крайних случаев забвение того факта, что ненерциальность системы связана с действием материальных сил на не менее материальное тело, движущееся ускоренно и несущее на себе неинерциальную систему координат создаёт иллюзию нематериальности (фиктивности) действующих в этой системе сил инерции.
Следует отметить, что этим не ограничивается набор возможных видов сил инерции. Так особого рассмотрения заслуживают силы, возникающие из-за неравномерности вращения системы отсчёта; от движения тел во вращающейся системе отсчёта , когда вектор скорости имеет составляющую, не параллельную оси вращения (Кориолисова сила); сама неинерциальная система может двигаться с переменной скоростью и потому уравнение движения тела в ней будет иметь вид дифференциального уравнения третьего и более высокого прядка и т.д.
I Движение тела в прямолинейно движущейся неинерциальной СО
[править]или
Для рассмотрения этого случая будет использован Рис.2
Неинерциальность системы вызвана воздействием на материальное тело с массой являющейся физическим носителем считающейся неинерциальной системы координат силы , создаваемой внешними по отношению к этому телу полями или телами.Поскольку это воздействие рассматривается в инерциальной системе координат, к этому воздействию применим без каких-либо оговорок Второй закон Ньютона, на основании которого это тело и, соответственно и связанная с ним система координат получает ускорение:
(13)
Дважды продифференцировав по времени обе части равенства (8) , получаем:
(14), где:
- есть ускорение тела в инерциальной СО, далее называемое абсолютным ускорением.
Это ускорение может быть измерено путём установки на наблюдаемом теле акселерометра, нуль которого установлен в ИСО, что гарантирует получение информации об абсолютном ускорении тела в ИСО. Если разместить и на материальном теле, с которым связана неинерциальная система отсчёта акселерометр , то и он, также будет показывать испытываемое собой ускорение, поскольку это тело ничем не отличается от тела наблюдаемого.
- есть ускорение неинерциальной СО в инерциальной СО, далее называемое переносным ускорением.
Это ускорение может быть измерено путём установки на теле, несущем неинерциальную систему отсчёта, акселерометра, нуль которого установлен также в ИСО, что гарантирует получение информации о переносном ускорении несущего тела и, соответственно, неинерциальной системы отсчёта в ИСО.
- есть ускорение тела в неинерциальной СО, далее называемое относительным ускорением.
Это ускорение может быть измерено путём вычитания переносного ускорения из абсолютного:
- (15)
Технически это может быть осуществлено изменением установки нуля акселерометра на наблюдаемом теле на величину переносного ускорения.
Использование акселерометров не обязательно, а ускорения могу быть измерены с использованием неконтактных методов, например путём измерения изменения частоты отражаемых волн (звуковых или электромагнитных) на основании эффекта Допплера.
Важно, что вся информация, полностью достаточная для получения представления о величине возникающей силы инерции может быть получена без участия наблюдателя современными методами телеметрии и обработки сигнала. Наблюдатель, с его субъективными оценками того, что фиктивно, а что-реально и представлениями об удобстве вычислений, совершенно не нужен
Относительное ускорение вполне реально[1] в неинерциальной СО, поскольку разница двух реальных величин в правой части уравнения (15 ) не может быть не реальной.
Умножим обе части уравнения (15) на массу тела и получим:
(16)
Тогда первый член в уравнении (16)называется абсолютной силой.
.(17)
Это - единственная сила, действующая на тело в первой (инерциальной) СО . Она продолжает действовать на тело с неизменной величиной в любой системе координат. Если на наблюдаемом теле будет находиться акселерометр, то его показания, полученные, скажем методом телеметрии также буду одинаковы для наблюдателей в любой из систем координат.
Следующая сила, определяемая как:
(18)
В соответствии с названием входящего в её определение ускорением, она будет силой переносной.
Следует обратить внимание на то обстоятельство, что она получена расчётным путём, а не путём непосредственного её измерения. Хотя и она не потребовала вмешательства наблюдателя и получена введением в объективное счётно-решающее устройство известной величины массы наблюдаемого тела и ускорения неинерциальной системы
Именно её влияние на картину движения тела во второй ,ускоренно движущейся системе координат, является камнем преткновения при попытке понять смысл понятия о силе инерции.Особенность переносной силы состоит в том, что,не действуя непосредственно на рассматриваемое тело, она вызывает появление силы инерции, которая действует и на него, и на всё, что находится в этой системе однообразным образом.
Физический смысл переносной силы состоит в том, что она представляет собой ту силу, которая действовала бы на наблюдаемое тело в том случае, если бы оно было неподвижно в неинерциальной системе (или само было бы носителем этой системы)
Перенося выражения для абсолютной и переносной силы в (16) в левую часть равенства:
(19)
и применяя введённые обозначения, получаем:
(20)
Входящее в правую часть относительное ускорение измеряется объективно аксеклерометрами, размещёнными на движущемся теле независимо от ускорения, испытываемого неинерциальной системой отсчёта, а масса в рамках классической физики не зависит от действующих на тело сил, правая часть в выражении (20) есть относительная сила, то есть сила, вызывающая ускорение тела в движущейся системе отсчёта.
(21)
Отсюда видно, что по причине действия переносной силы на материальное тело, являющееся носителем неинерционной системы отсчёта, в новой системе отсчёта на тело действует не полная сила , но лишь её часть , оставшаяся после вычитания из неё переносной силы так, что:
(22)
Ускорение, получаемое в результате действия силы может быть измерено акселерометром, установленным и на теле-носителе второй системы отсчёта. Таким образом объективно и беспристрастно действующая аппаратура, без вмешательства наблюдателя показывает, что на движущееся в неинерциальной системе тело одновременно , в зависимости от системы отсчёта, действуют две отличающиеся по величине силы. и .
Для того, чтобы отличить эти силы, действующие на тело от сил инерции, их иногда называют "Активными силами" ( [4] Стр.142)
Сохраняя материалистический взгляд на явления природы, остаётся заключить, что эта разница может возникнуть только потому, что , кроме абсолютной силы в неинерциальной системе на тело реально действует ещё некая сила , которая, будучи добавлена к абсолютной силе, порождает силу, вызывающую ускорение тела в его неинерциальной системе так, что
(23)
Используя формулы (23) и (22), получаем:
(24)
Видно, что эта сила направлена в противоположную сторону от силы, вызывающей ускорение неинерциальной системы и, вместе с ней, и находящегося в ней тела. Таким образом она соответствует необходимому признаку , дающего право назвать эту силу силой инерции. И потому она иногда называется эйлеровой силой инерции
Следует особенно подчеркнуть, что эта существование эйлеровой силы инерции подтверждается проделанным мысленным экспериментом на основании анализа показаний приборов. Поэтому нередко встречаемое утверждение, что эта сила "фиктивна" и вводится исключительно ради удобства вычислений, не имеет под собой никакого основания.
Существенно, что все математические соотношения, приведённые выше, позволили бы с использованием современной экспериментальной и вычислительной техники найти силу инерции для каждого реального случая без какого-либо вмешательства наблюдателя и учёта его субъективного взгляда на происходящее.
Обычно обсуждение появления эйлеровой силы инерции на этом заканчивается, поскольку ограничиваются констатацией факта наличия силы, действующей на носитель НСО, не уточняя её происхождения. Это имеет смысл в случае, если эта сила представляет собой результат воздействия поля, например моля гравитационного. Однако в случае, когда причиной этого ускорения является контактная сила, а носителем НСО является тело с массой, сравнимой с массой наблюдаемого тела и, обращая внимание, что на основании (13) и (18) речь идёт об одном и том же ускорении, можно пройти дальше, используя для вычисления переносного ускорения формулу (13)
(25)
Итак, Эйлерова сила инерции , возникающая в неинерциальной СО и представляющая собой разницу между относительной и абсолютной силами равна взятой с обратным знаком силе, вызывающей ускоренной движение НСО, взятой в отношении массы наблюдаемого тела к массе тела, несущего неинерциальную систему
Примеры движения тела в неинерциальных системах отсчёта
[править]Пусть масса лифта будет , а наблюдаемого тела .На движение наблюдаемого тела не будет наложено никаких связей и единственной действующей на него силой будет сила тяжести.На лифт же может, кроме силы тяжести, действовать и сила . Направление сил будет положительным, если они направлены вверх.
Тогда абсолютной силой будет: (26 )
а переносной силой (27)
В таком случае на наблюдаемое тело в НСО будет действовать эйлерова сила инерции (28):
(29)
а относительная сила, действующая на наблюдаемое тело в НСО будет равна:
(30)
Пример 1 Пусть . То есть лифт движется с постоянной скоростью или просто неподвижен в ИСО. Тогда по (29) эйлерова сила отсутствует. Действительно, при этом лифт не имеет в ИСО ускорения, т.е. принадлежит к бесчисленному семейству инерциальных систем координат, ничем друг от друга не отличающихся и имеющих общий признак -отсутствие эйлерова ускорения.
Наблюдаемое же в лифте тело падает вниз, что показывает выражение (30) для относительной силы , ставшей при этом и абсолютной силой (26)
Пример 2 Пусть . То есть лифт свободно падает под действием силы тяжести.Тогда наблюдаемое тело не испытывает в системе координат, связанной с лифтом никакой силы, потому что эйлерова сила инерции по (29 ) уравновешивает действующую на та тело абсолютную силу
В некоторых случаях , могут наблюдаться парадоксальные явления. Так, если лифт падает с ускорением, превышающим ускорение свободного падения , выпущенные из рук пассажира предметы будут падать на потолок кабины лифта.
Пример 3

Пассажир едет в автомобиле с постоянной скоростью в первой(инерциальной) системе отсчёта.На него в направлении движения не действуют никакие силы.И потому его абсолютное ускорение отсутствует . При резком торможении на его систему отсчёта (автомобиль) начинает действовать сила торможения, вызывающая её переносное ускорение в направлении, обратном направлении движения. Поскольку никаких внешних сил , действующих на пассажира при этом не возникает и абсолютное ускорение остаётся нулевым, его относительное ускорение оказывается равным по величине и обратным по направлению ускорению переносному, т.е направленным по направлению движения автомобиля.В этом же направлении действует на пассажира и эйлерова сила инерции Эта сила, вызывающая деформацию стекла и вызывает её разрушение.
II Силы инерции во вращающихся системах координат
[править]В рассмотренных выше случаях возникновения сил инерции имелась возможность указать на их первопричину. Ею были силы, не действующие непосредственно на наблюдаемое тело, но на тело, принятое за носителя неинерциальной системы отсчёта.
Существенным отличием в возникновении сил инерции во вращающихся системах координат и причиной возникновения сил инерции является сама неинерциальная система, ставшая таковой при её раскрутке и сохранившая первоначально полученный момент количества движения
Примером такого взаимодействия является , например, система, состоящая из планеты и её спутника.(Рис 3 )
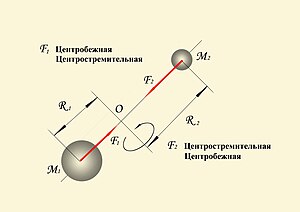
При допущении о том, что участвующие в таком движении небесные тела можно рассматривать, как материальные точки, единственной силой , которую можно принять во внимание, является сила взаимного гравитационного притяжения. Если же тело представлено ничем между собой не связанных коллективом материальных точек, то оно не может сохранять свою форму при вращении. Это произойдёт как следствие Третьего закона Кеплера, согласно которому квадраты перидов обращения двух разноудалённых точек относятся как кубы их расстояния от центра притяжения ([4] Стр.280).
Поэтому любое вращающееся тело может сохранять свою форму только благодаря силам, действующим между его частями. Эти же силы поддерживают его вращение, если абсолютные размеры тела настолько малы, что силы взаимного притяжения не могут обеспечить сохранение его формы.
Использование термина «центробежная сила» ( которой здесь является ньютонова сила инерции) правомочно тогда, когда точкой её приложения является не испытывающее поворот тело, а ограничивающее его движение связи. В этом смысле центробежная сила представляет собой один из членов в формулировке третьего закона Ньютона, антагониста центростремительной силе, вызывающей поворот рассматриваемого тела и к нему приложенной. Обе эти силы равны по величине и противоположны по направлению, но приложены к разным телам и потому не компенсируют друг друга, а вызывают реально ощутимый эффект — изменение направление движения тела (материальной точки).

Возможны два альтернативных подхода к рассмотрению вопроса о силах, действующих на тело, находящееся на поверхности вращающегося Земного шара.в соответствие с двумя способами размещения наблюдателя : В ИСО за пределами Земли и в НСО на Земле.Как предложено в [1] объектом наблюдения в каждом случае удобно рассматривать свободно подвешенный на нити груз.
В первом случае наблюдатель помещается вне Земли — в системе отсчёта, неподвижной по отношению к оси собственного вращения Земли и, скажем, какой-либо далёкой звезды — геоцентрической системе отсчёта[11]. Такая СО, если пренебречь движением Земли вокруг Солнца и движением Солнечной системы в целом, часто рассматривается в качестве модели инерциальной системой отсчёта (ИСО)
Предположим, что вначале Земля не вращается. Тогда груз висит на нити, которая под действием единственной в этом примере силы тяжести направлена к центру Земли и имеет ускорение Затем Земля, как карусель начинает вращение.Груз на нити, сохраняя состояние покоя, отстаёт и его расстояние от оси вращения в плоскости, перпендикулярной оси увеличивается. Нить деформируется за счёт своего растяжения и возникает сила, заставляющая груз следовать за точкой своего подвеса и, следовательно, за движением Земли.Благодаря отставанию груза и увеличения его расстояния от оси угол между нитью и, следовательно, силой приложенной нитью к телу, создающей ускорение и силой, тяжести становится меньше .Поэтому возникает по правилу параллелограмма центростремительное ускорение (зелёный вектор), заставляющее тело двигаться по окружности, если угловая скорость вращения будет оставаться постоянной.
В другом (альтернативном) случае, наблюдатель, совместно с изучаемым телом, принимает участие во вращении Земли. В этой системе отсчёта он видит, что висящий груз неподвижен и знает, что на него действуют сила тяжести,[12] , создающая ускорение
Кроме того он экспериментально устанавливает величину ускорения силы тяжести для данного места и отклонение нити подвеса от вертикали и это даёт ему основании вычислить направление и величину вектора центростремительного ускорения (синий вектор), как:. .Справа уравнении стоит разность двух реальных во всех отношениях величин. И сделать заключение, что слева в этом уравнении стоит величина несуществующая,фиктивная, сотворённая ради удобства вычислений, значит впасть в мистику.
Груз на нити остаётся в неподвижности из-за того, что действующая на него сила тяжести уравновешена по Третьему закону Ньютона силой деформации нити: Отметим также, что относительное значение центробежной силы невелико: на экваторе, где такое значение максимально, её вклад в силу тяжести составляет ~0,3 %[13]. Тем не менее можно представить себе поверхность, для которой во всех её точках нить будет направлена вертикадьно. Такой поверхностью будет обладать эллипсоид вращения. И это подтверждается точными измерениями формы Земного шара, радиус которого в направлении на полюс на несколько километров меньшне экваториального радиуса.
Общий подход к нахождению сил инерции
[править]Сравнивая движение тела в инерциальной и неинерциальной СО можно прийти к следующему выводу( [5]Страница 134):
Пусть есть сумма всех сил, действующих на тело в неподвижной (первой) системе координат, которая вызывает его ускорение . Эта сумма находится путём измерения ускорения тела в этой системе, если известна его масса.
Аналогично, есть сумма сил, измеренная в неинерциальной системе координат (второй), вызывающая ускорение , в общем случае отличающееся от вследствие ускоренного движения второй СО относительно первой.
Тогда сила инерции в неинерциальной системе координат будет определяться разницей:
(27)
или:
(28)
В частности, если тело покоится в неинерциальной системе, то есть , то
(29) ([1] стр. 134)>.
Итак, для измерения эйлеровой силы в неинерциальной системе координат следует найти сумму сил, действующих на тело в системе координат, принимаемой за неподвижную (инерционную) и при том уравновешивают силы инерции, действующие в ускоренно движущейся(неинерциальной) системе координат [1] стр. 134)
Трудность состоит в том, что нельзя одновременно находиться и в ИСО и в НСО. И не всегда удаётся решить, у какой из этих систем ведётся в данный момент наблюдение движения тела. Утверждать, что таковой является ИСО можно лишь тогда, когда имеется полная уверенность, что все действующие на тело активные силы учтены и движение тела полностью объясняется ими.
В связи с этим величину эйлеровой силы можно получить,измерив переносную силу, которая ей равна по величине и противопложна по направлению.(См.(23))
Движение тела по произвольной траектории в неинерциальной СО
[править]Положение материального тела в условно неподвижной и инерциальной системе задаётся здесь вектором , а в неинерциальной системе — вектором . Расстояние между началами координат определяется вектором . Угловая скорость вращения системы задаётся вектором , направление которого устанавливается по оси вращения по правилу правого винта. Линейная скорость тела по отношению к вращающейся СО задаётся вектором .
В данном случае ускорение тела в инерционной (первой) системе отсчёта, в соответствии с (11), будет равно сумме:
(30) [14]
- первый член — переносное ускорение второй системы относительно первой;
- второй член — ускорение, возникающее из-за неравномерности вращения системы вокруг своей оси;
- третий член — Кориолисово ускорение, вызванное той составляющей вектора скорости, которая не параллельна оси вращения неинерциальной системы;
- последний член представляет собой центростремительное ускорение и, одновременно , относительное ускорение тела во второй (неинерциальной) системе отсчёта
Общее уравнение механики (к вопросу о реальности сил инерции)
[править]В неинерциальной системе отсчёта принцип Даламбера -Лагранжа формулируется так :
Если к действующим на точки механической системы активным силам присоединить силы инерции , то при при движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ активных сил и элементарных работ сил инерции на любом возможном перемещении системы равна нулю. (Цитируется по Физический энциклопедический словарь/ Гл. ред. А.М.Прохоров. Ред.кол. Д.М.Алексеев, А.М. Бонч-Бруевич,А.С.Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил. Страница 142)
Таким образом представление о реальности сил инерции (точнее эйлеровых сил) входит в основные положения современной механики.
Вместе с тем существует противоположное мнение о том, что силы инерции работы не совершают , и являются всего лишь удобным вычислительным приёмом и потому не существуют в реальности (фиктивны) [15]).
Хотя силы инерции существуют по крайней мере со времени образования Солнечной системы, т.е. задолго до того, как кому-то потребовалось записывать уравнения движения.
Кстати, для того, чтобы заметить замедление хода маятников часов при перемещении в низкие широты вообще не требуется записывать уравнения движения. Достаточно лишь своевременно эти часы заводить.
При этом вопрос о силах инерции напрямую связан с вопросом об универсальности Второго закона и его применимости к объяснению движения тела в неинерциальных системах отсчёта. Реальность сил инерции однозначно подтверждает это положение ([5] Страница 133) Все приведённые выше примеры показывают, что силы инерции , векторно взаимодействуя с обычными силами и, в ряде случаев, компенсируя их действие, ведут себя также, как и обычные силы, вызванные непосредственным (контактным) взаимодействием тел или же полями.
Работа сил инерции
[править]В инерциальной системе возникающие в ней ньютоновы силы инерции работы не совершают.
Учёт работы эйлеровых сил в неинерциальной системе отсчёта , наравне с силами обычного происхождения в формулировке Принципа Даламбера закрывает дискуссию не только о возможности совершения ими работы, но и причисления их к "фиктивным силам вводимым для удобства вычислений". Ибо созданный умозрительно фиктивный физический фактор не может принимать участие в совершении работы.
Эйлеровы силы инерции могут совершать работу, хотя возможна и ситуация, когда они присутствуют, но работы не совершают. Так эти силы совершают работу, связанную с удлинением спиц велосипедного колеса при его раскручивании и прекращают при достижении установившейся скорости вращения ([1] страницы 105 - 115).
Примером работы, совершаемой Кориолисовой силой в планетарном масштабе является эффект Бэра. Правда, впоследствии А.Эйнштейн показал, что проявления этого эффекта преувеличены . Однако вызванные силами Кориолиса пассаты и океанические течения совершают работу, заметно влияющую на климатические явления в планетарном масштабе.
При решении задач на бумаге, когда искусственно сводят динамическую задачу движения к задаче статики, вводят третий вид сил, называемый силами Даламбера, работы не совершающих, поскольку работа и неподвижность тел, несмотря на действие на него сил в физике есть понятия несовместимые.
Равновесие механической системы
[править]Для свободного тела, то есть тела, на которое не наложено никаких связей, условие равновесия в декартовой системе координат определяется равенством нулю сумм проекций действующих на каждый компонент системы сил на координатные оси и сумм всех приложенных к телу моментов сил относительно этих осей:
(1)
и (2)
Выполнение этих условий будет свидетельствовать о том, что избранная система отсчёта инерциальна и потому в этой системе отсчёта тело будет либо покоиться, либо двигаться без поворота (в том числе и вращения) равномерно и прямолинейно.([4] Стр.601)
Но выполнения этих условий недостаточно для того, чтобы равновесие сохранялось независимо от внешних воздействий на систему. Для этого необходимо, чтобы оно было устойчивым.
Равновесие системы считается устойчивым, если при малом нарушении её консервативности, т.е изменении суммы её кинетической и потенциальной энергий ([4] Стр.309) путём воздействия извне, её компоненты мало отклоняются от равновесного положения и возвращаются в него после прекращения воздействия.
Для консервативных систем достаточное условие равновесия системы определяется теоремой Лагранжа-Дирихле, согласно которой равновесие устойчиво, если положение её равновесия соответствует минимуму потенциальной энергии([4] Стр.797).
Механические связи
[править]Если же тело несвободно по причине наложенных на него связей, те из формул (1) и (2), которые не относятся к реакциям связей, будут определять равновесие системы. Остальные уравнения дают сведения, позволяющие определить реакции связей, что становится возможным в том случае, если связи жёстко закрепляют систему, препятствуя любым в ней движениям.([4] Стр.601). В противном случае необходимость учёта реакций связи и внесения их в уравнение движения создаёт далеко не всегда решаемую проблему.[1]
Принцип возможных перемещений
[править]Изменение состояния механической системы определяется изменением её координат, определяющих число степеней свободы. Во многих случаях их число ограничено связями, путём силового воздействия на компоненты системы препятствующими некоторым изменениям. Оставшиеся возможности изменения координат определяются возможными перемещениями.
Принцип возможных перемещений представляет собой один из вариационных принципов в науке о движении тел. Он устанавливает общее условие равновесия механической системы. При этом под равновесием понимается такое состояние механической системы, подверженной влиянию сил, при котором все образующие систему материальные точки не меняют своего положения, то есть покоятся по отношению к этой системе. Если это равновесие наблюдается в инерциальной системе, такое равновесие называется абсолютным, в неинерциальной системе равновесие будет лишь относительным.([4] Стр.601)
Этот принцип гласит:
Для равновесия механической системы с идеальными (не совершающими работы) связями необходимо и достаточно, чтобы сумма работ всех приложенных к системе активных сил на любом возможном перемещении системы была равно нулю([4] Стр.81)
(3)
есть элементарная работа, совершаемая «активными силами» направленными под углом к направлению виртуального смещения
Оговорка об активных силах предусматривает отсутствие сил инерции, то есть рассмотрение возможных перемещений в инерциальной системе отсчёта.
Существенно, что в число активных сил входят и реакции связей трудно, а в некоторых случаях вообще не поддающихся математическому описанию. В этом случае оказывается эффективным введение в рассмотрение абсолютно жёстких связей , не деформируемых и потому не совершающих работы. Как и инерциальные системы отсчёта, такие связи являются абстракцией, приемлемой только при условии, что происшедшие от их принятия ошибки не превышают оговорённого ранее значения. Но, предположив, что связи абсолютно жестки, можно при решении проблемы равновесия механической системы с точки зрения принципа возможных перемещений вообще исключить из рассмотрения реакции связи.([1] Стр.178 −189)
Основной закон динамики
[править]Включает в свою формулировку упоминание о совершаемой силами инерции работе, наравне с работой, совершаемой обычными силами. Сила инерции — термин, широко применяемый в физике. Понятие о работе силы инерции входит в основной закон динамики:
(1)
или иначе :
(2)
Здесь : есть элементарная работа, совершаемая «активными силами» — индекс x=a (то есть силами, происхождение которых можно в принципе проследить) и силами инерции индекс — x=j (то есть силами, возникшими благодаря воздействию других активных сил не на сам i-тый компонент системы, но на систему отсчёта, что в результате изменило его ускорение.)
В (2) предполагается, что работа вызвана силой , направленной под углом для активной силы и под углом для силы инерции к направлению виртуального смещения
Общее уравнение механики учитывает работу сил инерции наравне с работой активных сил. Это значит, что с позиции общих принципов механики в отношении сил инерции (точнее сил инерции) «…следует признать, что у нас нет сколько-нибудь веских оснований сомневаться в реальности сил инерции…»
([1] Стр.178)
Вместе с тем под силой инерции понимаются совершенно разные силы.
Общее уравнение механики представляет собой математическую формулировку принципа Д’Аламбера — Лагранжа, дающего общий метод решения задач динамики и статики и являющегося одним из основных принципов теоретической механики.([4] Стр.142) Этот принцип объединяет принцип возможных перемещений и принцип Д'Аламбера
Принцип Даламбера
[править]В случае рассмотрения механических систем, не находящихся в состоянии равновесия, реакции связи игнорировать нельзя. Однако, при сохранении допущения об абсолютной жёсткости этих связей, оказывается, что при этом понятие связи лишилось физического содержания и исчезла возможность выразить реакции связей как функции координат .([1] Стр.178 −189)Следовательно невозможно и записать дифференциальные уравнения движения.
Выход из создавшегося затруднения был предложен Даламбером.:
Записывается Второй Ньютона в форме:
= + (4)
Где к силе, действующей на тело добавляется сила реакции связей
Затем производится перенос всех членов равенства налево:
( — ) + = 0 (5)
Возникает видимость равновесия сил, позволяющая формально применить принцип возможных перемещений. И потому и здесь стало возможным не принимать во внимание силы реакции связей .([1] Страница 183)
Но сила (- ) есть не что иное, как сила противодействия из Третьего закона Ньютона или же ньютонова сила инерции, не приложенная к телу. Здесь же она благодаря искусственному приёму к этому телу приложена. Таким образом создана парадоксальная ситуация, заключающаяся в том, что на тело действуют взаимно компенсирующие силы, но тело, тем не менее, движется с ускорением.
Поэтому сила (- ), которая носит название даламберова сила инерции в силу того, что не является следствием объективных физических процессов, но продуктом субъективной воли, безусловно фиктивна.([1] Стр.178 −189)
Принцип Даламбера-Лагранжа
[править]Вначале Принцип Д’Аламбера не содержал никакого упоминания о силах инерции. Но со временем под вектором (- ) стали понимать силу инерции[16](Ссылка в[1] Стр.131).
В механической системе с идеальными связями сумма элементарных работ, совершаемых активными силами и силами инерции на любом возможном (виртуальном) перемещении равна нулю.
Общее уравнение механики учитывает работу сил инерции наравне с работой активных сил. Это значит, что с позиции общих принципов механики в отношении сил инерции (точнее эйлеровых сил инерции) «…следует признать, что у нас нет сколько-нибудь веских оснований сомневаться в реальности сил инерции…»([1] Стр.178)
Даламберовы силы инерции
[править]Изменение состояния механической системы определяется изменением её координат, определяющих число степеней свободы. Во многих случаях их число ограничено связями, путём силового воздействия на компоненты системы препятствующими некоторым изменениям. Оставшиеся возможности изменения координат определяются возможными перемещениями. Уравнения связей могу зависеть от времени, в них могут входить не только координаты, но и скорости, наконец, силы реакции связи могут производить работу. ([4] Стр.672 ).
Ниже будут рассматриваться связи, не зависящие от времени (стационарные), не зависящие от скоростей (голономные) и связи, сумма элементарных работ которых на любом возможном перемещении равна нулю (связи идеальные)([4] Страница 672.Тема "Связи механические")
Составление уравнений движения с учётом реакций связей представляет собой трудную, подчас невыполнимую работу и потому целесообразно располагать способом вообще исключения связей из рассмотрения.
В этом полезным оказывается вариационный принцип -принцип возможных перемещений .Суть которого состоит в том, что "для равновесия механической системы с идеальными связями необходимо и достаточно , чтобы сумма работ приложенных к системе сил на любом возможном перемещении была равна нулю".([4] Стр.81).Здесь речь идёт о системе, находящейся в ИСО , где могут существовать лишь ньютоновы силы инерции, в уравнения движения составляющих систему тел не входящие.
Решение вопроса основано во введение в рассмотрение абсолютно жёстких связей. ( Разумется настолько жёстких, что их с заданной малой погрешностью можно считать таковыми). При этом используется тот факт, что сила реакции абсолютно жёсткой связи не совершает работы и потому при применении к системе с такими связями появляется возможность исключить вообще реакции связи из рассмоторния.
Но при введении представления об абсолютно жёстких связях понятие силы реакции лишается физического содержания. Что не даёт возможности вычислить реакции связи как функции координат и скорости. Вследствие этого невозможно и составит дифференциальных уравнений движения.([4] Стр.179-180)
Принцип Даламбера, в форме, данной Лагранжем даёт способ решить проблему следующим образом : Записывается Второй Ньютона в форме:
= + (13)
Где к силе, действующей на тело добавляется сила реакции связей
Затем произодится перенос всех членов равенства налево:
( - ) + = 0 (14)
Снова возникает видимость равновесия сил, позволяющая применить принцип возможных перемещений.Но силы реакции связей оказываются из уравнений движения исключёнными. ([5] Страница 183)
Вначале [Принцип Д’Аламбера ]] не содержал никакого упоминания о силах инерции.Но со временем под вектором - ) стали понимать силу инерции [16](Ссылка в [4] Стр.131). Повторилась рассмотренная выше ситуация, когда ньютоновы силы инерции, мысленно перенесены с ускоряющих тел, на которые они фактически действуют, на тело ускоряемое, на которое они фактически не действуют. В общем случае они влияли на связи, но здесь их влияние (работа) из-за их абсолютной жёсткости равна нулю.
Это побуждает рассматривать такие Даламберовы силы инерции , как бесспорно фиктивные.([5] Страница 188). Их невозможно измерить физической аппаратурой и потому они отсутствуют в Природе
Эквивалентность сил инерции и гравитации
[править]Примечания
[править]- ↑ а б в г д е ё ж з и й к л м н о п р с т у ф х ц ч ш щ ъ ы Хайкин С. Э. Силы инерции и невесомость. — М.: Наука, 1967. Ошибка цитирования Неверный тег
<ref>: название «ХСЭ» определено несколько раз для различного содержимого - ↑ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
- ↑ В конкретно заданной системе координат. При переходе в другую систему направление нередко может измениться
- ↑ а б в г д е ё ж з и й к л м н о п Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич,А. С. Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил. Ошибка цитирования Неверный тег
<ref>: название «ФЭС» определено несколько раз для различного содержимого - ↑ а б в г д е ё ж з Страница 127
- ↑ а б А. Ю. Ишлинский. Классическая механика и силы инерции. «Наука», 1987. С. 15.
- ↑ В конкретно заданной системе координат. При переходе в другую систему направление нередко может измениться
- ↑ Помимо во многом сознательно культивируемого отсутствия чёткости в подчёркивании принципиальной разницы между тремя указанных выше сил инерции , существует и широко распространено ошибочное мнение. Оно заключается в утверждении, что к описанию движения тел в неинерциальных системах (НСО) Второй закон Ньютона неприменим. При этом нигде и никогда не сообщается, какой в этом случае более общий закон природы описывает реально наблюдаемые механические закономерности в этой системе. Таким образом количественные закономерности связи между ускорением, испытываемым телом и действующей на него силой , экспериментально наблюдаемые в реальной действительности, оказываются не облечёнными в форму законов Природы.
- ↑ В космических масштабах причинно-следственной связи может и не быть ввиду конечной скорости распространения любого силового взаимодействия, что является исходным положением специальной теории относительности
- ↑ А. Ю. Ишлинский. Классическая механика и силы инерции. «Наука», 1987. С. 18.
- ↑ Геоцентрические системы координат
- ↑ Тарг С. М. Сила тяжести // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 496. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8
- ↑ Н. П. Грушинский. Основы гравиметрии. — М.: «Наука», 1983. — С. 34. — 351 с.
- ↑ , Walter Greiner Klassische Mehanik II.Wissenschaftlicher Verlag Harri Deutsch GmbH. Frankfurt am Main.2008 ISBN 978-3-8171-1828-1
- ↑ А. Ю. Ишлинский. Классическая механика и силы инерции. «Наука», 1987.
- ↑ а б Николаи Е. Л. сборник «Труды Ленинградского индустриального института» № 6,1936, ОНТИ, Ленинград Ошибка цитирования Неверный тег
<ref>: название «Николаи» определено несколько раз для различного содержимого





































































![{\displaystyle {\vec {a_{r}}}={\frac {d^{2}{\vec {R}}}{dt^{2}}}+{\frac {d{\vec {\omega }}}{dt}}\times {\vec {r^{\prime }}}+{2{\vec {\omega }}\times {\vec {v}}}+{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {r^{\prime }}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cf4bd94f826de3291695bdadd9890669b9a29ad)












